Các câu hỏi tương tự
Cho biểu thức
f
(
x
)
1
2018
x
+
2018
. Tính tổng
S
2018
[
f
(
-
2017
)
+
f
(
-
2016
)
+
.
.
.
...
Đọc tiếp
Cho biểu thức f ( x ) = 1 2018 x + 2018 . Tính tổng
S = 2018 [ f ( - 2017 ) + f ( - 2016 ) + . . . + f ( 0 ) + f ( 1 ) + . . . + f ( 2018 ) ]
![]()
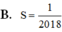
![]()
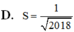
Cho hàm số f(x) có đạo hàm trên R và thỏa mãn f(2016) a, f(2017) b,
a
;
b
∈
ℝ
. Giá trị
I
∫
2017
2016
2015
f
x
.
f
2014
x
d
x
bằng: A.
I
b
2017...
Đọc tiếp
Cho hàm số f(x) có đạo hàm trên R và thỏa mãn f(2016) = a, f(2017) = b, a ; b ∈ ℝ . Giá trị I = ∫ 2017 2016 2015 f ' x . f 2014 x d x bằng:
A. I = b 2017 - a 2017
B. I = a 2016 - b 2016
C. I = a 2015 - b 2015
D. I = b 2015 - a 2015
Giải bất phương trình 2016 x + 2016 1 - x ≤ 2017
A. 1 ≤ x ≤ 2016
B. 0 ≤ x ≤ 1
C. x ≤ 1 hoặc x ≥ 2016
D. x ≤ 0 hoặc x ≥ 1
Hỏi có bao nhiêu giá trị nguyên x trong đoạn [-2017; 2017] thỏa mãn bất phương trình
log
3
x
-
log
5
x
≤
log
3
x
.
log
5
x
A. 2017 B. 4026 C. 2018 D. 2016
Đọc tiếp
Hỏi có bao nhiêu giá trị nguyên x trong đoạn [-2017; 2017] thỏa mãn bất phương trình log 3 x - log 5 x ≤ log 3 x . log 5 x
A. 2017
B. 4026
C. 2018
D. 2016
Cho hàm số
f
(
x
)
a
x
4
+
b
x
2
+
c
v
ớ
i
a
0
,
c
2017
,
a
+
b
+
c
2017
.
Số cực trị của hàm...
Đọc tiếp
Cho hàm số f ( x ) = a x 4 + b x 2 + c v ớ i a > 0 , c > 2017 , a + b + c < 2017 . Số cực trị của hàm số y = | f ( x ) - 2017 | là
A. 1
B. 5
C. 3
D. 7
Cho hàm số f(x) xác định trên R{1} thỏa mãn
f
(
x
)
1
x
-
1
,
f
(
0
)
2017
;
f
(
2
)
2018
. Tính S f(3)-f(-1) A. S 1 B. S ln2 C. S ln4035 D. S 4
Đọc tiếp
Cho hàm số f(x) xác định trên R\{1} thỏa mãn f ' ( x ) = 1 x - 1 , f ( 0 ) = 2017 ; f ( 2 ) = 2018 . Tính S = f(3)-f(-1)
A. S = 1
B. S = ln2
C. S = ln4035
D. S = 4
Giải bất phương trình
1
2
x
2
2
x
. Gọi tập nghiệm là S. Tìm S. A. (-1;0) B.
0
;
+
∞
C. (0;1) D. Rỗng
Đọc tiếp
Giải bất phương trình 1 2 x 2 > 2 x . Gọi tập nghiệm là S. Tìm S.
A. (-1;0)
B. 0 ; + ∞
C. (0;1)
D. Rỗng
Số nghiệm thực của phương trình
x
5
+
x
x
2
-
2
-20170 A. 4 B. 5 C. 2 D. 3
Đọc tiếp
Số nghiệm thực của phương trình
x 5 + x x 2 - 2 -2017=0
A. 4
B. 5
C. 2
D. 3
Cho hàm số
f
x
a
x
4
+
b
x
2
+
c
với
a
0
,
c
2017
và
a
+
b
+
c
2017
. Số cực trị của hàm số
y
f
x
−...
Đọc tiếp
Cho hàm số f x = a x 4 + b x 2 + c với a > 0 , c > 2017 và a + b + c < 2017 . Số cực trị của hàm số y = f x − 2017 là
A. 1
B. 5
C. 3
D. 7



