\(y'=\dfrac{3}{\left(x+2\right)^2}>0\Rightarrow\) hàm đồng biến trên đoạn đã cho
\(\Rightarrow\max\limits_{\left[0;1\right]}y=y\left(1\right)=0\)
Giá trị lớn nhất và nhỏ nhất của hàm số y = 5 x + 5 1 - x trên đoạn [0;1] là:
A. m i n 0 ; 1 y = 2 5 ; m a x 0 ; 1 y = 6
B. m i n 0 ; 1 y = 2 5 ; m a x 0 ; 1 y = 5
C. m i n 0 ; 1 y = 2 ; m a x 0 ; 1 y = 6
D. m i n 0 ; 1 y = 2 ; m a x 0 ; 1 y = 5
Cho hàm số y = f(x) liên tục trên đoạn [0;1] thoả mãn ∫ 0 1 x 2 f ( x ) d x = 0 và m a x [ 0 ; 1 ] f ( x ) = 6 Giá trị lớn nhất của tích phân ∫ 0 1 x 3 f ( x ) d x bằng
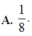
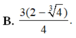
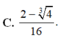
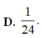
Cho hàm số y = f(x) nhận giá trị không âm và liên tục trên đoạn [0;1]. Đặt g ( x ) = 1 + 2 ∫ 0 x f ( t ) d t . Biết g ( x ) ≥ f 3 ( x ) . Tích phân ∫ 0 1 g 2 ( x ) 3 d x có giá trị lớn nhất bằng
A. 5/3.
B. 4.
C. 4/3.
D. 5.
Cho a và b là hai số dương. Tìm giá trị lớn nhất của hàm số y = x a ( 1 - x ) b trên [0;1]
A. y = a a b b a + b a b
B. y = a b b a a + b a b
C. y = a a b b a + b a + b
D. y = a b b a a + b a + b
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x 2 - 3 x + 6 x - 2 trên đoạn [0;1]. Giá trị của M + 2m bằng
A. -11
B. -10
C. 11
D. 10
Cho hàm số y = f (x) có đạo hàm liên tục trên đoạn [0;1] thỏa mãn f(0)=1; ∫ 0 1 ( 1 - x ) 2 f ' ( x ) d x = 1 3 . Giá trị nhỏ nhất của tích phân bằng ∫ 0 1 f 2 ( x ) d x bằng
Cho hàm số f(x) có đạo hàm là f'(x). Đồ thị của hàm số y = f'(x) được cho như hình vẽ dưới đây:
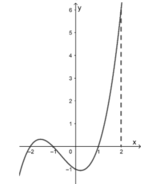
Biết rằng f(-1) + f(0) < f(1) + f(2). Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = f(x) trên đoạn [-1;2] lần lượt là:
A. f(1);f(2)
B. f(2);f(0)
C. f(0);f(2)
D. f(1);f(-1)
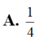
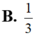
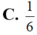
Cho hàm số y = f(x) có đạo hàm liên tục trên đoạn [0;1] thoả mãn 3 f ( x ) + x f ' ( x ) ≥ x 2018 Giá trị nhỏ nhất của tích phân ∫ 0 1 f ( x ) d x bằng
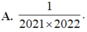
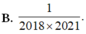
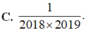
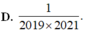
Cho hàm số y = x + 1 x - 1 . Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số trên đoạn [-5;-1]. Tính M + m
A. -6
B. 2 3
C. 3 2
D. 6 5
