Các câu hỏi tương tự
Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
-
1
+
2
.
cos
x
2
-
3
.
sin
x...
Đọc tiếp
Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = - 1 + 2 . cos x 2 - 3 . sin x + cos x trên ℝ . Biểu thức M + N + 2 có giá trị bằng:
A. 0
B. 4 2 - 3
C. 2
D . 2 + 3 + 2
Tập hợp các giá trị của m để phương trình \(2\cos^2x-sinx+1-m=\)0 có đúng 5 nghiệm thuộc \([0;\frac{5\pi}{2})\)là nửa khoảng (a;b]. Tính tổng a + b.
AB là đoạn vuông góc chung của 2 đường thẳng
∆
,
∆
chéo nhau,
A
∈
∆
;
B
∈
∆
, AB a. M là điểm di động trên
∆
N là điểm di động trên
∆
. Đặt
A
M
m
;
A
N
n
(
m
≥...
Đọc tiếp
AB là đoạn vuông góc chung của 2 đường thẳng ∆ , ∆ ' chéo nhau, A ∈ ∆ ; B ∈ ∆ ' , AB= a. M là điểm di động trên ∆ N là điểm di động trên ∆ ' . Đặt A M = m ; A N = n ( m ≥ 0 ; n ⩾ 0 ) Giả sử ta luôn có m 2 + n 2 = b với b>0; b không đổi. Xác định m, n để độ dài đoạn MN đạt giá trị lớn nhất.
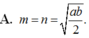
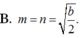
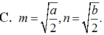
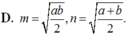
1. hàm số y = 3cosx luôn nhận giá trị trong tập nào
2. tập xác định của hàm số y = cosx
3. tính giới hạn \(L=\lim\limits\dfrac{n^2-3n^3}{2n^3+5n-2}\)
4. tính giới hạn \(L=\lim\limits\left(3n^2+5n-3\right)\)
5. kết quả của giới hạn \(\lim\limits_{n\rightarrow+\infty}\left(n^3-2n^2+3n-4\right)\)
Cho hàm số f(n) 1+3+6+10+...+
n
(
n
+
1
)
2
(
n
∈
N
*
)
. Biết lim
f
(
n
)
(
3
n
+
1
)...
Đọc tiếp
Cho hàm số f(n)= 1+3+6+10+...+ n ( n + 1 ) 2 ( n ∈ N * ) .
Biết lim f ( n ) ( 3 n + 1 ) ( 5 n 2 + 2 ) = a b ( a , b ∈ Z ) phân số này tối giản. Giá trị b - 5a là
A.50
B.45
C.85
D.60
1) cho dãy left(u_nright) xác định bởi u_n2.3^n giá trị của u_{20} với mọi số nguyên dương làA. 2.3^{19} B.2.3^{20} C.3^{20} D.2.3^{21}2) cho dãy left(u_nright) xác định bởi u_n3^n số hạng u_{n+1} làA. 3^n+1 B.3^n+3 C.3^n.3 D.3left(n+1right)3) cho dãy số left(u_nright) với u_n4^n+2^n ba số hạng đầu tiên của dãy là4) cho dãy số left(u_nright) n ϵ N* biết u_ndfrac{1}{n+1} ba số hạng đầu tiên của...
Đọc tiếp
1) cho dãy \(\left(u_n\right)\) xác định bởi \(u_n=2.3^n\) giá trị của \(u_{20}\) với mọi số nguyên dương là
A. 2.\(3^{19}\) B.\(2.3^{20}\) C.\(3^{20}\) D.\(2.3^{21}\)
2) cho dãy \(\left(u_n\right)\) xác định bởi \(u_n=3^n\) số hạng \(u_{n+1}\) là
A. \(3^n+1\) B.\(3^n+3\) C.\(3^n.3\) D.\(3\left(n+1\right)\)
3) cho dãy số \(\left(u_n\right)\) với \(u_n=4^n+2^n\) ba số hạng đầu tiên của dãy là
4) cho dãy số \(\left(u_n\right)\) n ϵ N* biết \(u_n=\dfrac{1}{n+1}\) ba số hạng đầu tiên của dãy số đó là
5) cho dãy số có các số hạng đầu tiên là 5,10,15,20,25,.. số hạng tổng quát của dãy số là
Tìm giá trị của m để phương trình \(\dfrac{sinx-m}{2cosx+\sqrt{3}}=0\) có đúng hai nghiệm thuộc \((0;\dfrac{5\pi}{2}]\)
tính giá trị biểu thức saua) Adfrac{25^6}{5^3}b) B32.left(dfrac{3}{2}right)^5c) Cleft(dfrac{1}{3}right)^4.3^{-3}d) D4^{-2}.left(dfrac{2}{5}right)^5.5^4e) E9^{-5}:left(dfrac{5}{3}right)^4.25^2f) Fleft(dfrac{5}{8}right)^{-2}:4^2g) Gleft(dfrac{5}{3}right)^3.left(dfrac{9}{2}right)^2:left(sqrt{3}right)^4
Đọc tiếp
tính giá trị biểu thức sau
a) \(A=\dfrac{25^6}{5^3}\)
b) \(B=32.\left(\dfrac{3}{2}\right)^5\)
c) \(C=\left(\dfrac{1}{3}\right)^4.3^{-3}\)
d) \(D=4^{-2}.\left(\dfrac{2}{5}\right)^5.5^4\)
e) \(E=9^{-5}:\left(\dfrac{5}{3}\right)^4.25^2\)
f) \(F=\left(\dfrac{5}{8}\right)^{-2}:4^2\)
g) \(G=\left(\dfrac{5}{3}\right)^3.\left(\dfrac{9}{2}\right)^2:\left(\sqrt{3}\right)^4\)
Cho n
≥
2, n
∈
N thỏa mãn :
A
n
3
+
C
n
2
14
n
. Giá trị của n là A. 3. B. 4. C. 5. D. 6.
Đọc tiếp
Cho n ≥ 2, n ∈ N thỏa mãn : A n 3 + C n 2 = 14 n . Giá trị của n là
A. 3.
B. 4.
C. 5.
D. 6.
Cho hàm số
y
x
3
-
3
x
+
2
có đồ thị (C) . Gọi d là đường thẳng đi qua A(3;20) và có hệ số góc m. Giá trị của m để đường thẳng cắt (C) tại 3 điểm phân biệt là
Đọc tiếp
Cho hàm số y = x 3 - 3 x + 2 có đồ thị (C) . Gọi d là đường thẳng đi qua A(3;20) và có hệ số góc m. Giá trị của m để đường thẳng cắt (C) tại 3 điểm phân biệt là
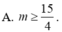
