Các câu hỏi tương tự
Cho hàm số yf(x) có đạo hàm liên tục trên R và có đồ thị hàm số yf (x) như hình vẽ bên. Xét hàm số g(x)f(x^2-3) và các mệnh đề sau:1. Hàm số g(x) có 3 điểm cực trị.2. Hàm số g(x)đạt cực tiểu tại x 0.3. Hàm số g(x)đạt cực đại tại x 2.4. Hàm số g(x)đồng biến trên khoảng (-2;0).5. Hàm số g(x)nghịch biến trên khoảng (-1;1). Có bao nhiêu mệnh đề đúng trong các mệnh đề trên? A. 1. B. 4. C. 3. D. 2.
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f' (x) như hình vẽ bên. Xét hàm số g(x)=f(x^2-3) và các mệnh đề sau:

1. Hàm số g(x) có 3 điểm cực trị.
2. Hàm số g(x)đạt cực tiểu tại x = 0.
3. Hàm số g(x)đạt cực đại tại x = 2.
4. Hàm số g(x)đồng biến trên khoảng (-2;0).
5. Hàm số g(x)nghịch biến trên khoảng (-1;1).
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A. 1.
B. 4.
C. 3.
D. 2.
Cho
y
F
(
x
)
v
à
y
G
(
x
)
là những hàm số có đồ thị cho trong hình bên dưới, đặt
P
(
x
)
F
(
x
)
G
(
x
)
.
Tính
P
(...
Đọc tiếp
Cho y = F ( x ) v à y = G ( x ) là những hàm số có đồ thị cho trong hình bên dưới, đặt P ( x ) = F ( x ) G ( x ) . Tính P ' ( 2 ) .
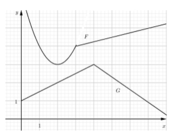
A. 5 2
B. 4
C. 3 2
D. 6
Cho hàm số yf(x) có đạo hàm trên R và có đồ thị yf’(x) như hình vẽ. Xét hàm số
g
(
x
)
f
(
x
2
-
2
)
Mệnh đề nào sau đây sai? A. Hàm số g(x) nghịch biến trên (0;2) B. Hàm số g(x) đồng biến trên (2;+∞) C. Hàm số g(x) nghịch biến trên (-∞;-2) D. Hàm số g(x) nghịch biến trên (-1;0)
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm trên R và có đồ thị y=f’(x) như hình vẽ. Xét hàm số g ( x ) = f ( x 2 - 2 )
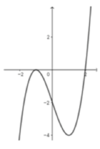
Mệnh đề nào sau đây sai?
A. Hàm số g(x) nghịch biến trên (0;2)
B. Hàm số g(x) đồng biến trên (2;+∞)
C. Hàm số g(x) nghịch biến trên (-∞;-2)
D. Hàm số g(x) nghịch biến trên (-1;0)
Cho hàm số yf(x) liên tục trên R và thỏa mãn f(-1)0f(0). Gọi S là diện tích hình phẳng giới hạn bởi các đường yf(x),y0,x-1 và x1. Mệnh đề nào sau đây đúng? A.
S
∫
-
1
0
f
(
x
)
d
x
+
∫
0
1
|
f
(
x
)
|
d
x...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R và thỏa mãn f(-1)>0<f(0). Gọi S là diện tích hình phẳng giới hạn bởi các đường y=f(x),y=0,x=-1 và x=1. Mệnh đề nào sau đây đúng?
A. S = ∫ - 1 0 f ( x ) d x + ∫ 0 1 | f ( x ) | d x
B. S = ∫ - 1 1 | f ( x ) | d x
C. S = ∫ - 1 1 f ( x ) d x
D. S = ∫ - 1 1 f ( x ) d x
Cho hai hàm số
f
(
x
)
a
x
4
+
b
x
3
+
c
x
2
+
d
x
+
e
với
a
≠
0
và g(x)
p
x
2
+
q
x
-
3
c
ó
đồ thị như...
Đọc tiếp
Cho hai hàm số f ( x ) = a x 4 + b x 3 + c x 2 + d x + e với a ≠ 0 và g(x)= p x 2 + q x - 3 c ó đồ thị như hình vẽ bên dưới. Đồ thị hàm số y=f(x) đi qua gốc tọa độ và cắt đồ thị hàm số y=g(x) tại bốn điểm có hoành độ lần lượt là -2;-1;1 và m. Tiếp tuyến của đồ thị hàm số y=f(x)-g(x) tại điểm có hoành độ x=-2 có hệ số góc bằng -15/2. Gọi (H) là hình phẳng giới hạn bởi đồ thị hai hàm số y=f(x) và y=g(x) (phần được tô đậm trong hình vẽ). Diện tích của hình (H) bằng

A. 1553 120
B. 1553 240
C. 1553 60
D. 1553 30
Cho hàm số yf(x) có đạo hàm trên R. Đường cong trong hình vẽ bên là đồ thị của hàm số yf’(x),(yf’(x) liên tục trên R). Xét hàm số
g
x
f
x
2
-
2
. Mệnh đề nào dưới đây sai? A. Hàm số g(x) nghịch biến trên (-∞;-2). B. Hàm số g(x) đồng biến trên (2;+∞). C. Hàm số g(x)nghịch biến trên(-1;0). D. Hàm số g(x) ngh...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm trên R. Đường cong trong hình vẽ bên là đồ thị của hàm số y=f’(x),(y=f’(x) liên tục trên R). Xét hàm số g x = f x 2 - 2 . Mệnh đề nào dưới đây sai?
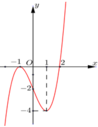
A. Hàm số g(x) nghịch biến trên (-∞;-2).
B. Hàm số g(x) đồng biến trên (2;+∞).
C. Hàm số g(x)nghịch biến trên(-1;0).
D. Hàm số g(x) nghịch biến trên (0;2).
Cho hàm số y f (x) xác định trên R và có đạo hàm f’(x) thỏa f’(x) (1–x)(x+2)g(x)+2018 với g(x) 0,
∀
x
∈
R
. Hàm số y f(1 – x) + 2018x + 2019 nghịch biến trên khoảng nào? A.
1
;
+
∞
B.
0
;...
Đọc tiếp
Cho hàm số y = f (x) xác định trên R và có đạo hàm f’(x) thỏa f’(x) = (1–x)(x+2)g(x)+2018 với g(x) < 0, ∀ x ∈ R . Hàm số y = f(1 – x) + 2018x + 2019 nghịch biến trên khoảng nào?
A. 1 ; + ∞
B. 0 ; 3
C. - ∞ ; 3
D. 3 ; + ∞
Cho hàm số y f(x) có đạo hàm liên tục trên R đồ thị hàm số y f’(x) như hình vẽ.Biết f(2) –6, f(–4) –10 và hàm số g(x) f(x)+
x
2
2
, g(x) có ba điểm cực trị. Phương trình g(x) 0? A. Có đúng 2 nghiệm B. Vô nghiệm C. Có đúng 3 nghiệm D. Có đúng 4 nghiệm
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm liên tục trên R đồ thị hàm số y = f’(x) như hình vẽ.
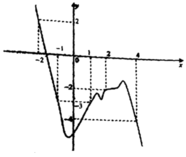
Biết f(2) = –6, f(–4) = –10 và hàm số g(x) = f(x)+ x 2 2 , g(x) có ba điểm cực trị.
Phương trình g(x) = 0?
A. Có đúng 2 nghiệm
B. Vô nghiệm
C. Có đúng 3 nghiệm
D. Có đúng 4 nghiệm
13/04 lúc 19:56
1.Tìm nghiệm của đa thức sau: h(y)=y^2-|y|
2.Cho g(x)=ax^2+bx+c có a,b,c thỏa mãn:3a+b=0
CMR:g(1).g(2) >= 0
giúp tớ nha!