\(\dfrac{5}{8}+\dfrac{3}{8}x=1\dfrac{1}{8}\)
\(\Rightarrow\dfrac{5}{8}+\dfrac{3}{8}x=\dfrac{9}{8}\)
\(\Rightarrow\dfrac{3}{8}x=\dfrac{9}{8}-\dfrac{5}{8}\)
\(\Rightarrow\dfrac{3}{8}x=\dfrac{4}{8}\)
\(\Rightarrow x=\dfrac{4}{8}:\dfrac{3}{8}\)
\(\Rightarrow x=\dfrac{4}{8}\cdot\dfrac{8}{3}=\dfrac{4}{3}\)
\(---\)
\(\dfrac{1}{2}-\left(\dfrac{1}{3}x-2\right)=\dfrac{2}{3}\)
\(\Rightarrow\dfrac{1}{3}x-2=\dfrac{1}{2}-\dfrac{2}{3}\)
\(\Rightarrow\dfrac{1}{3}x-2=-\dfrac{1}{6}\)
\(\Rightarrow\dfrac{1}{3}x=-\dfrac{1}{6}+2\)
\(\Rightarrow\dfrac{1}{3}x=\dfrac{11}{6}\)
\(\Rightarrow x=\dfrac{11}{6}:\dfrac{1}{3}\)
\(\Rightarrow x=\dfrac{11}{6}\cdot3=\dfrac{11}{2}\)
\(---\)
\(\left(3x+4\right)\left(2x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}3x+4=0\\2x-3=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}3x=-4\\2x=3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{4}{3}\\x=\dfrac{3}{2}\end{matrix}\right.\)
\(--\)
\(-4+4x=9x-14\)
\(\Rightarrow4x-9x=-14+4\)
\(\Rightarrow-5x=-10\)
\(\Rightarrow x=\left(-10\right):\left(-5\right)=2\)
\(---\)
\(\left\{\left[\left(\dfrac{1}{25}-0,6\right)^2:\dfrac{49}{125}\right]\cdot\dfrac{5}{6}\right\}-\left[\left(\dfrac{-1}{3}\right)+\dfrac{1}{2}\right]\)
\(=\left[\left(-\dfrac{14}{25}\right)^2\cdot\dfrac{125}{49}\right]\cdot\dfrac{5}{6}-\dfrac{1}{6}\)
\(=\left(\dfrac{196}{625}\cdot\dfrac{125}{49}\right)\cdot\dfrac{5}{6}-\dfrac{1}{6}\)
\(=\dfrac{4}{5}\cdot\dfrac{5}{6}-\dfrac{1}{6}\)
\(=\dfrac{4}{6}-\dfrac{1}{6}\)
\(=\dfrac{3}{6}\)
\(=\dfrac{1}{2}\)
\(Toru\)

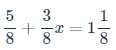
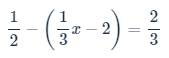
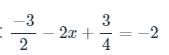
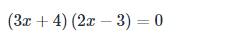
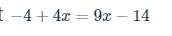
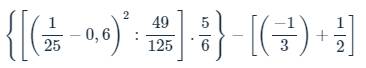 ghi kết quả thôi ạ , k phải trình bày ạ , e cần gấp ạ !!!!!
ghi kết quả thôi ạ , k phải trình bày ạ , e cần gấp ạ !!!!!



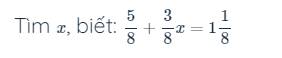
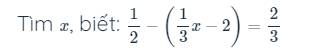
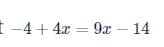
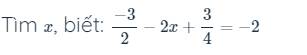
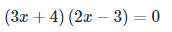 chỉ ghi kết quả thôi ah , k phải trình bày ra ah gấp ạ
chỉ ghi kết quả thôi ah , k phải trình bày ra ah gấp ạ


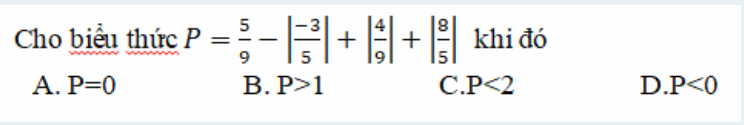


 ghi đáp án thôi ah , k phải trình bày ah
ghi đáp án thôi ah , k phải trình bày ah


 giúp mình bài 2.4 thôi ạ , mình cần gấp ạ
giúp mình bài 2.4 thôi ạ , mình cần gấp ạ

