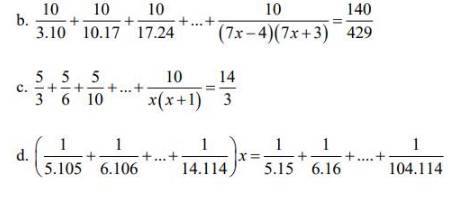b: \(\dfrac{10}{3\cdot10}+\dfrac{10}{10\cdot17}+...+\dfrac{10}{\left(7x-4\right)\left(7x+3\right)}=\dfrac{140}{429}\)
=>\(\dfrac{10}{7}\left(\dfrac{7}{3\cdot10}+\dfrac{7}{10\cdot17}+...+\dfrac{7}{\left(7x-4\right)\left(7x+3\right)}=\dfrac{140}{129}\right)\)
=>\(\dfrac{7}{3\cdot10}+\dfrac{7}{10\cdot17}+...+\dfrac{7}{\left(7x-4\right)\left(7x+3\right)}=\dfrac{140}{129}:\dfrac{10}{7}=\dfrac{98}{129}\)
=>\(\dfrac{1}{3}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{17}+...+\dfrac{1}{7x-4}-\dfrac{1}{7x+3}=\dfrac{98}{129}\)
=>\(\dfrac{1}{3}-\dfrac{1}{7x+3}=\dfrac{98}{129}\)
=>\(\dfrac{1}{7x+3}=\dfrac{1}{3}-\dfrac{98}{129}=\dfrac{-55}{129}\)
=>\(7x+3=-\dfrac{129}{55}\)
=>\(7x=-\dfrac{129}{55}-3=-\dfrac{294}{55}\)
=>\(x=-\dfrac{294}{55}:7=-\dfrac{42}{55}\)
c: \(\dfrac{5}{3}+\dfrac{5}{6}+...+\dfrac{10}{x\left(x+1\right)}=\dfrac{14}{3}\)
=>\(\dfrac{10}{6}+\dfrac{10}{12}+...+\dfrac{10}{x\left(x+1\right)}=\dfrac{14}{3}\)
=>\(10\left(\dfrac{1}{6}+\dfrac{1}{12}+...+\dfrac{1}{x\left(x+1\right)}\right)=\dfrac{14}{3}\)
=>\(\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{x\left(x+1\right)}=\dfrac{14}{30}\)
=>\(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{x}-\dfrac{1}{x+1}=\dfrac{7}{15}\)
=>\(\dfrac{1}{2}-\dfrac{1}{x+1}=\dfrac{7}{15}\)
=>\(\dfrac{1}{x+1}=\dfrac{1}{2}-\dfrac{7}{15}=\dfrac{1}{30}\)
=>x+1=30
=>x=29(nhận)