a: \(\dfrac{3}{2}\cdot4^x+\dfrac{5}{3}\cdot4^{x+2}=\dfrac{3}{2}\cdot4^8+\dfrac{5}{3}\cdot4^{10}\)
=>\(\dfrac{3}{2}\cdot4^x+\dfrac{5}{3}\cdot4^x\cdot16=\dfrac{3}{2}\cdot4^8+\dfrac{5}{3}\cdot4^8\cdot4^2\)
\(\Leftrightarrow4^x\left(\dfrac{3}{2}+\dfrac{5}{3}\cdot16\right)=4^8\left(\dfrac{3}{2}+\dfrac{5}{3}\cdot4^2\right)\)
=>\(4^x=4^8\)
=>x=8
b: \(\left(\dfrac{1}{2}-\dfrac{1}{3}\right)\cdot6^x+6^{x+2}=6^7+6^4\)
=>\(\dfrac{1}{6}\cdot6^x+6^x\cdot36=6^4\left(6^3+1\right)\)
=>\(6^x\left(36+\dfrac{1}{6}\right)=6^5\left(36+\dfrac{1}{6}\right)\)
=>\(6^x=6^5\)
=>x=5
c: \(\dfrac{1}{3}\cdot3^n=7\cdot3^2\cdot9^2-2\cdot3^n\)
=>\(3^n\cdot\dfrac{1}{3}+2\cdot3^n=7\cdot3^2\cdot3^4\)
=>\(3^n\cdot\dfrac{7}{3}=7\cdot3^6\)
=>\(3^n=7\cdot3^6:\dfrac{7}{3}=3^7\)
=>n=7
d: \(3\cdot5^{2x+1}-3\cdot25^x=300\)
=>\(3\cdot5^{2x}\cdot5-3\cdot5^{2x}=300\)
=>\(5^{2x}\cdot12=300\)
=>\(25^x=25\)
=>x=1
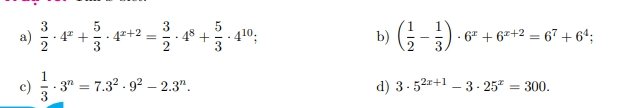
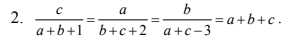tìm a, b, c