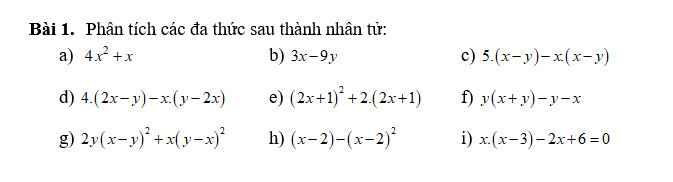a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)
Do đó: ADME là hình chữ nhật
a, Vì M,D là trung điểm BC,AB nên MD là đtb tg ABC
Do đó MD//AC\(\Rightarrow\)MD⊥AB(AC⊥AB)
\(\Rightarrow\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)
Vậy ADME là hcn
b, Vì E là trung điểm PM và AC nên AMCP là hbh
Mà PM⊥AC(ME⊥AC) nên AMCP là hthoi
c, Để AMCP là hv thì \(\widehat{AMC}=90^0\) hay AM là đường cao
Mà AM là trung tuyến tg ABC
Vậy AMCP là hình vuông khi tg ABC vuông cân tại A












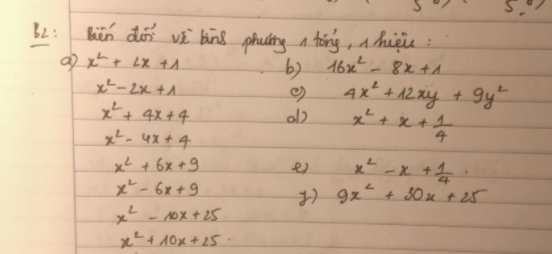




 em cần giải gấp bài 3 chi tiết mọi người giúp em với ạ. Làm bài dưới dạng phân số ạ em cần gấp
em cần giải gấp bài 3 chi tiết mọi người giúp em với ạ. Làm bài dưới dạng phân số ạ em cần gấp