a: ĐKXĐ: \(x\notin\left\{4;-4\right\}\)
b: \(A=\left(\dfrac{4}{x-4}-\dfrac{4}{x+4}\right)\cdot\dfrac{x^2+8x+16}{32}\)
\(=\dfrac{4\left(x+4\right)-4\left(x-4\right)}{\left(x-4\right)\left(x+4\right)}\cdot\dfrac{\left(x+4\right)^2}{32}\)
\(=\dfrac{32}{\left(x-4\right)}\cdot\dfrac{x+4}{32}=\dfrac{x+4}{x-4}\)
c: Để A=1/3 thì \(\dfrac{x+4}{x-4}=\dfrac{1}{3}\)
=>3(x+4)=x-4
=>3x+12=x-4
=>2x=-16
=>x=-8(nhận)
d: Để A là số nguyên thì \(x+4⋮x-4\)
=>\(x-4+8⋮x-4\)
=>\(8⋮x-4\)
=>\(x-4\in\left\{1;-1;2;-2;4;-4;8;-8\right\}\)
=>\(x\in\left\{5;3;6;2;8;0;12;-4\right\}\)
Kết hợp ĐKXĐ, ta được: \(x\in\left\{5;3;6;2;8;0;12\right\}\)











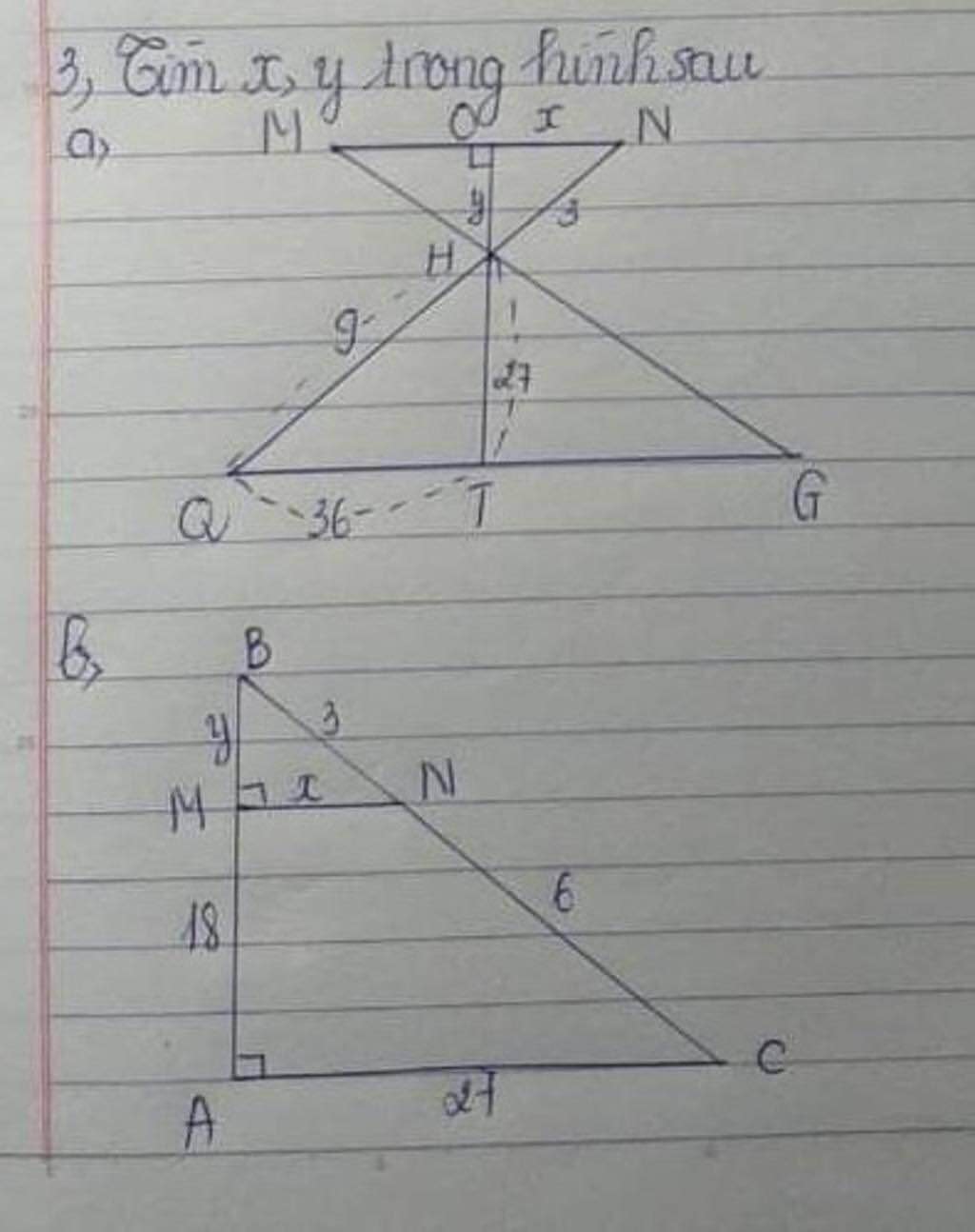

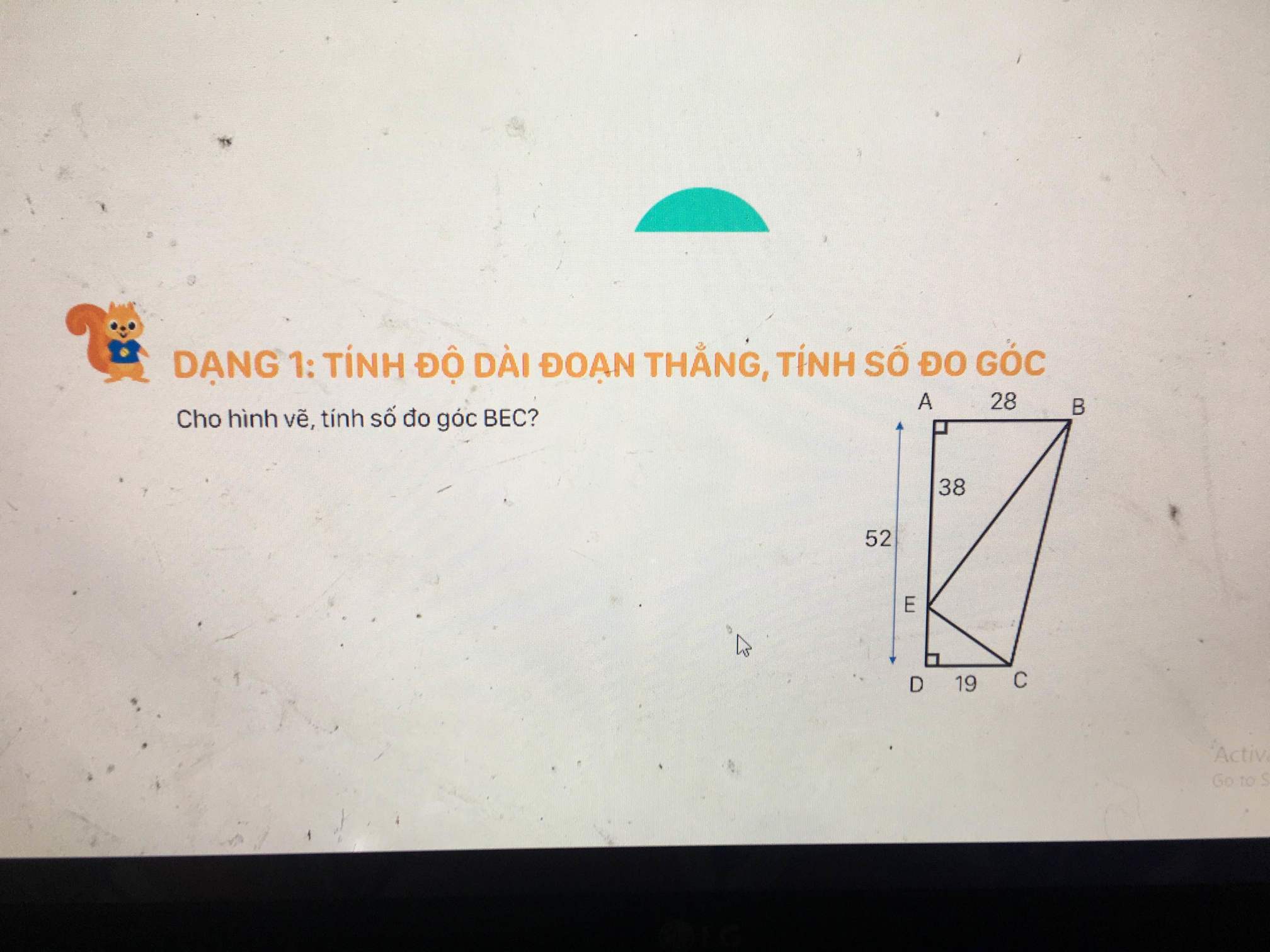



 EM ĐANG CẦN GẤP, MỌI NGƯỜI GIÚP EM!!!
EM ĐANG CẦN GẤP, MỌI NGƯỜI GIÚP EM!!!




