\(B=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{x-1}\right):\left(\dfrac{2}{x}-\dfrac{2-x}{x\left(\sqrt{x}+1\right)}\right)\)
\(=\left(\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\left(\dfrac{2\left(\sqrt{x}+1\right)}{x\left(\sqrt{x}+1\right)}-\dfrac{2-x}{x\left(\sqrt{x}+1\right)}\right)\)
\(=\left(\dfrac{x+2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\left(\dfrac{x+2\sqrt{x}}{x\left(\sqrt{x}+1\right)}\right)\)
\(=\dfrac{\left(x+2\sqrt{x}\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{x\left(\sqrt{x}+1\right)}{\left(x+2\sqrt{x}\right)}=\dfrac{x}{\sqrt{x}-1}\)
\(B=2\Rightarrow\dfrac{x}{\sqrt{x}-1}=2\Rightarrow x-2\sqrt{x}+2=0\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)^2+1=0\) (vô nghiệm)
Vậy ko tồn tại x thỏa mãn
c.
\(B=\dfrac{x}{\sqrt{x}-1}=\sqrt{x}-1+\dfrac{1}{\sqrt{x}-1}+2\ge2\sqrt{\dfrac{\sqrt{x}-1}{\sqrt{x}-1}}+2=4\)
\(B_{min}=4\) khi \(x=4\)
a: Ta có: \(B=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{x-1}\right):\left(\dfrac{2}{x}-\dfrac{2-x}{x\left(\sqrt{x}+1\right)}\right)\)
\(=\dfrac{x+\sqrt{x}+\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}:\dfrac{2\left(\sqrt{x}+1\right)-2+x}{x\cdot\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\sqrt{x}-1}\cdot\dfrac{x}{2\sqrt{x}+2-2+x}\)
\(=\dfrac{x}{\sqrt{x}-1}\)
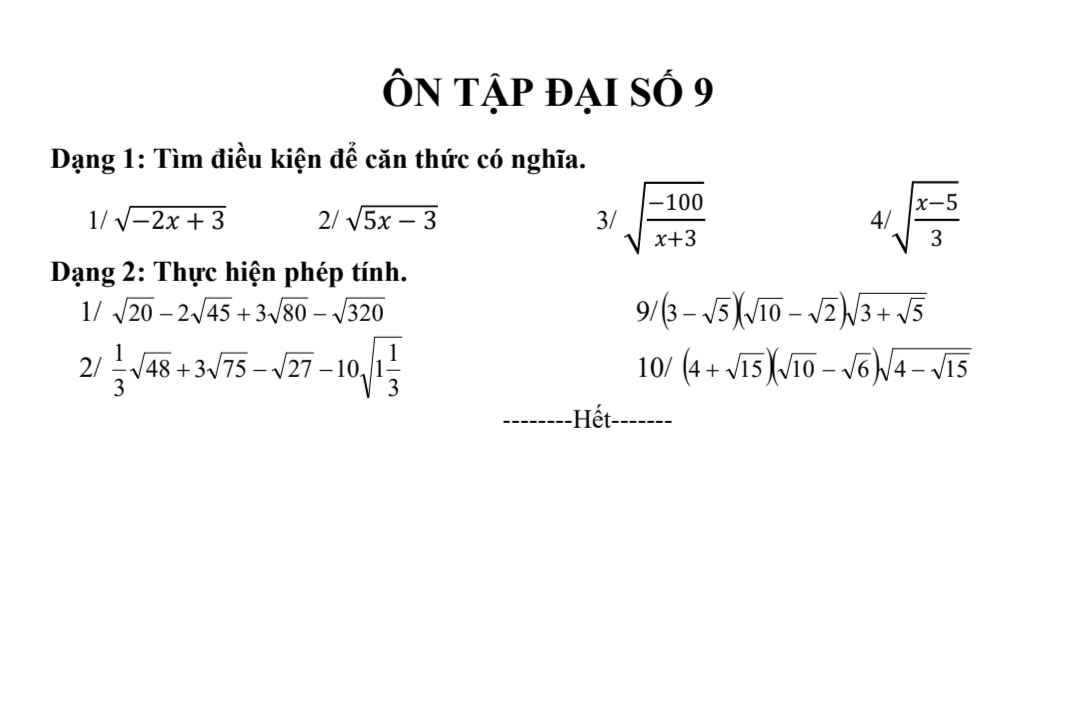
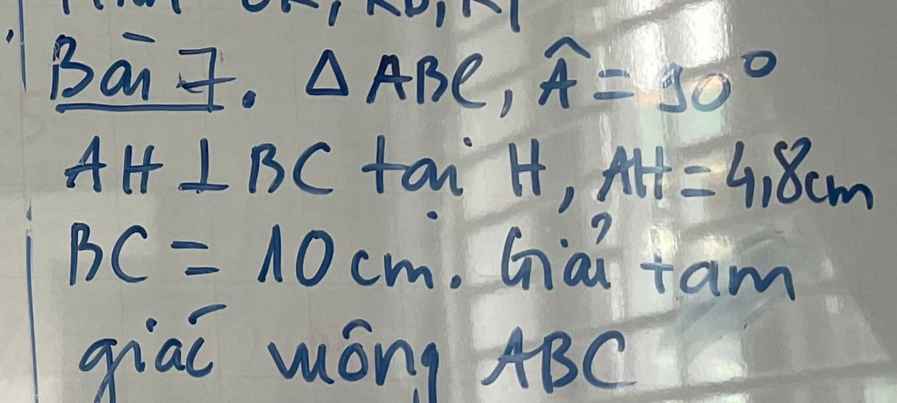
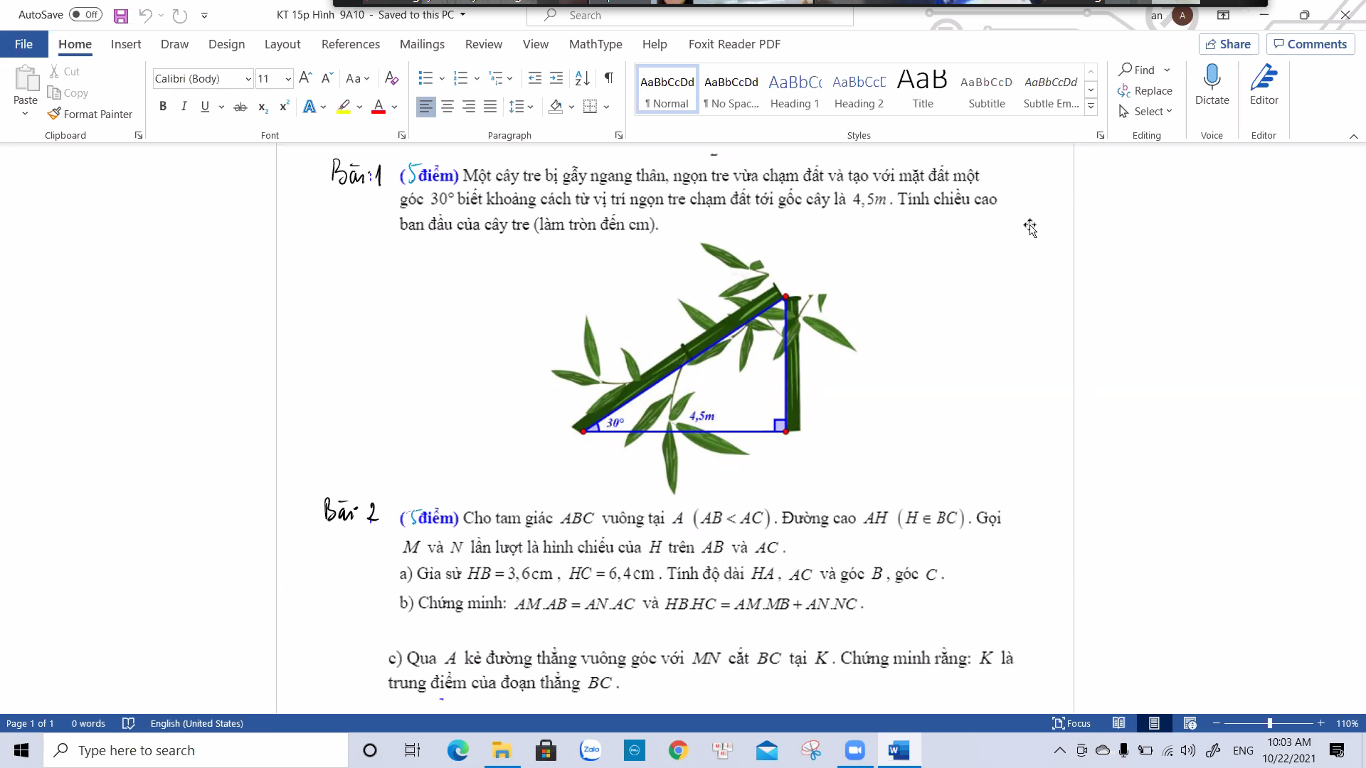
Ai giúp em với ạ em cần rất gấp bài 4 thôi ạ
em cần giải gấp bài 2 ạ, mọi người giúp em với ạ
giúp em với ạ, cần gấp ạ TvT