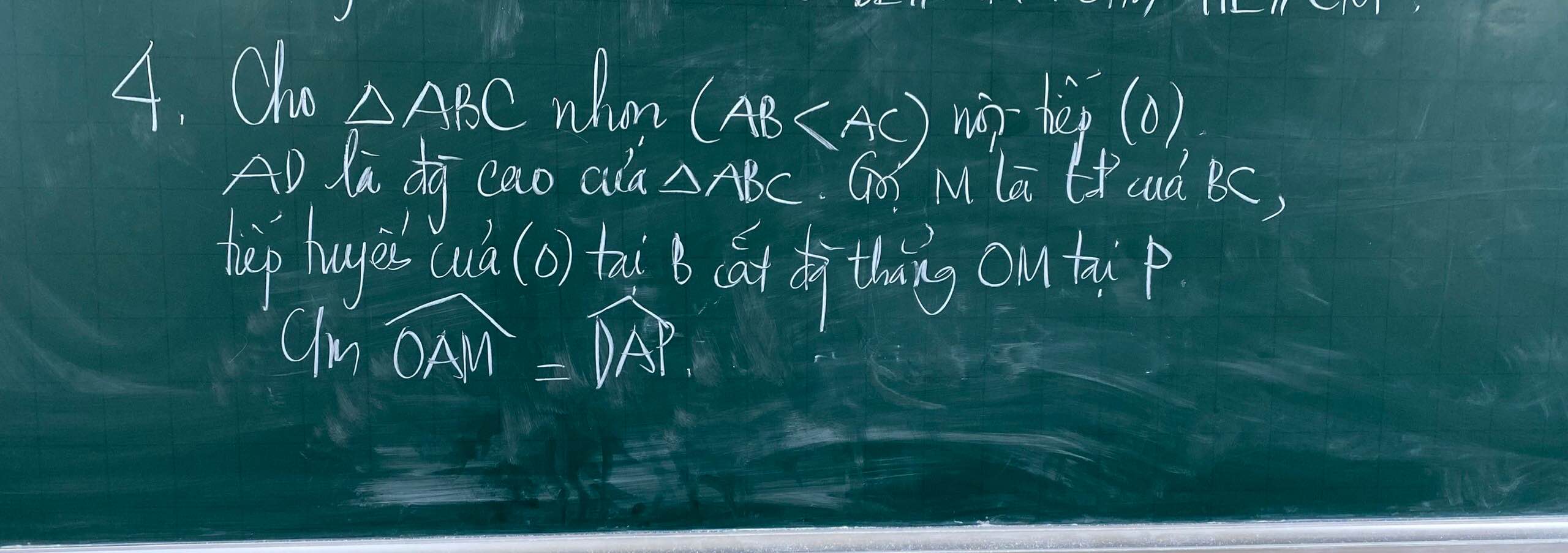Question

E đang cần trước 18h á mn giúp e với

Answer 1

ΔOBC cân tại O

mà OM là đường trung tuyến
nên OM⊥BC tại M

Xét ΔOBP vuông tại B có BM là đường cao

nên \(OM\cdot OP=OB^2\)

=>\(OM\cdot OP=OA^2\)

=>\(\frac{OM}{OA}=\frac{OA}{OP}\)

Xét ΔOMA và ΔOAP có

\(\frac{OM}{OA}=\frac{OA}{OP}\)

góc MOA chung

Do đó: ΔOMA~ΔOAP

=>\(\hat{OAM}=\hat{OPA}\) (1)

ta có: OM⊥BC

AD⊥BC

Do đó: OM//AD

=>OP//AD

=>\(\hat{OPA}=\hat{DAP}\) (hai góc so le trong)(2)

Từ (1),(2) suy ra \(\hat{OAM}=\hat{DAP}\)