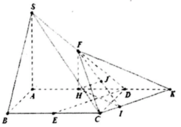
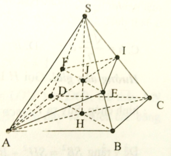
a: Ta có: SA\(\perp\)(ABCD)
AB,AD\(\subset\)(ABCD)
Do đó: SA\(\perp\)AB và SA\(\perp\)AD
=>ΔSAB vuông tại A; ΔSAD vuông tại A
Ta có: DC\(\perp\)SA(SA\(\perp\)(ABCD))
DC\(\perp\)DA(ABCD là hình vuông)
SA,AD cùng thuộc mp(SAD)
Do đó: DC\(\perp\)(SAD)
=>DC\(\perp\)SD
=>ΔSDC vuông tại D
b: Ta có: AH\(\perp\)SD
DC\(\perp\)AH(DC\(\perp\)(SAD))
SD,DC cùng thuộc mp(SDC)
Do đó: AH\(\perp\)(SDC)
=>AH\(\perp\)SC
Ta có: AB\(\perp\)AD(ABCD là hình vuông)
AB\(\perp\)SA(SA\(\perp\)(ABCD))
AD,SA cùng thuộc mp(SAD)
Do đó:AB\(\perp\)(SAD)
mà SD\(\subset\)(SAD)
nên AB\(\perp\)SD
mà SD\(\perp\)AH
và AB,AH cùng thuộc mp(ABH)
nên SD\(\perp\)(ABH)
=>SD\(\perp\)BH