Đáp án B
Hàm số bậc nhất trên bậc nhất y = a x + b c x + d ; c ≠ 0 luôn có duy nhất một tiệm cận ngang y = a c
Như vậy hàm số đã cho y = 2 x − 6 x − 2 có tiệm cận ngang là y = 2 ⇔ y − 2 = 0
Đáp án B
Hàm số bậc nhất trên bậc nhất y = a x + b c x + d ; c ≠ 0 luôn có duy nhất một tiệm cận ngang y = a c
Như vậy hàm số đã cho y = 2 x − 6 x − 2 có tiệm cận ngang là y = 2 ⇔ y − 2 = 0
Cho hàm số y = a x + 1 b x - 1 b ≠ 0 , a + b ≠ 0 có đồ thị (C). Biết đồ thị (C) có tiệm cận ngang là đường thẳng y = 2. Khi đó tỉ số a/b là:
A. 3
B. 2
C. -1
D. 1
Cho a là một số thực dương khác 1. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau:
1. Hàm số y= l o g a x có tập xác định là D= ( 0 ; + ∞ ) .
2. Hàm số y= l o g a x là hàm đơn điệu trên khoảng ( 0 ; + ∞ ) .
3. Đồ thị hàm số y= l o g a x và đồ thị hàm số y = a x đối xứng nhau qua đường thẳng y= x.
4. Đồ thị hàm số y= l o g a x nhận Ox là một tiệm cận
A. 4
B. 1
C. 3
D. 2
Xét các mệnh đề sau
(1). Đồ thị hàm số y = 1 2 x - 3 có hai đường tiệm cận đứng và một đường tiệm cận ngang
(2). Đồ thị hàm số y = x + x 2 + x + 1 x có hai đường tiệm cận ngang và một đường tiệm cận đứng
(3). Đồ thị hàm số y = x - 2 x - 1 x 2 - 1 có một đường tiệm cận ngang và hai đường tiệm cận đứng.
Số mệnh đề đúng là:
A. 0
B. 3
C. 2
D. 1
Cho hàm số y = f(x) có đồ thị như hình vẽ dưới đây:
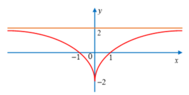
Trong các khẳng định sau:
I. Đồ thị hàm số có tiệm cận ngang là đường thẳng y = 2
II. Hàm số đạt cực tiểu tại x = -2
III. Hàm số nghịch biến trong khoảng − ∞ ; 0 và đồng biến trong khoảng 0 ; ∞
IV. Phương trình f(x) = m có hai nghiệm phân biệt khi và chỉ khi . Có bao nhiêu khẳng định đúng
A. 1
B. 2
C. 3
D. 4
Biết rằng đồ thị hàm số y = a x + 1 b x - 2 có đường tiệm cận đứng là x = 2 và đường tiệm cận ngang là y = 3. Tính giá trị của a + b?
A.1
B.5
C.4
D.0
Biết rằng đồ thị hàm số y = a x + 1 b x - 2 có đường tiệm cận đứng là x = 2 và đường tiệm cận ngang là y = 3. Tính giá trị của a + b.
A. a + b = 1
B. a + b = 5
C. a + b = 4
D. a + b = 0
Tìm số phát biểu đúng trong các phát biểu sau:
(1) Đồ thị hàm số y= x α với α > 0 nhận trục Ox làm tiệm cận ngang và nhận trục là tiệm cận đứng.
(2) Đồ thị hàm số y= x α với α > 0 không có tiệm cận.
(3) Đồ thị hàm số y = log a x với 1 < a ≠ 1 nhận trục Oy làm tiệm cận đứng và không có tiệm cận ngang.
(4) Đồ thị hàm số y=ax với 1 < a ≠ 1 nhận trục Ox làm tiệm cận ngang và không có tiệm cận đứng.
A. 2.
B. 1
C. 4
D. 3.
Cho hàm số y=f(x) xác định trên R thỏa mãn lim f x x → - ∞ = 1 ; lim f x x → + ∞ = 1 và f(x)=1<=>x=0. Tổng số đường tiệm cận đứng và ngang của đồ thị hàm số y = 1 f x - 1 là
A. 2
B. 1
C. 4
D. 3
Cho hàm số y=f (x) liên tục trên R thỏa mãn l i m x → - ∞ f ( x ) = 0 ; l i m x → + ∞ f ( x ) = 1 . Tổng số đường tiệm cận đứng và ngang của đồ thị hàm số đã cho là:
A. 2
B. 1
C. 3
D. 0
Số đường tiệm cận của đồ thị hàm số y = x + 1 x 2 - a ( 0 < a ≠ 1 ) là
A. 0
B. 1
C. 3
D. 4