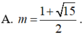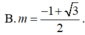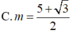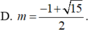Dựa vào tam giác Pa-xcan:C17 = 7; C27 = 21
C28 = C17 + C27 = 7 + 21 = 28
1 + 2 +⋯+ 7 = ((1 + 7).7)/2 = 28
⇒ 1 + 2 +⋯+ 7 = C28
Dựa vào tam giác Pa-xcan:C17 = 7; C27 = 21
C28 = C17 + C27 = 7 + 21 = 28
1 + 2 +⋯+ 7 = ((1 + 7).7)/2 = 28
⇒ 1 + 2 +⋯+ 7 = C28
Dùng tam giác Pa-xcan, chứng tỏ rằng 1 + 2 + 3 + 4 = C 5 2
cho a,b,c là 3 cạnh của 1 tam giác có chu vi bằng 4. chứng minh rằng: \(a^2+b^2+c^2+abc< 8\)
cho a,b,c là 3 cạnh của 1 tam giác có chu vi bằng 4. chứng minh rằng \(a^2+b^2+c^2+abc< 8\)
Bài 6. Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau. Kẻ OH vuông góc với mp(ABC)
tại H. Chứng minh rằng
a) OA⊥BC,OB⊥AC,OC⊥AB
b) Gọi K là giao điểm của AH với BC. Chứng minh rằng AK⊥BC
c) Gọi M là giao điểm của CH với AB. Chứng minh rằng AB⊥MC . Từ đó suy ra H là trực tâm tam giác
ABC.
d)
Bài 7. Cho hình chóp SABCD có đáy ABCD là hình chứ nhật có SA vuông góc với mp(ABCD). Chứng minh
rằng các mặt bên của hình chóp là các tam giác vuông.
Bài 8. Cho hình chóp SABCD có đáy ABCD là hình thang vuông tại A và D với AD=DC=AB/2 . Gọi I là trung điểm của đoạn AB, SA vuông góc với mặt đáy. Chứng minh rằng
a) Tam giác ABC vuông tại C
b) CI⊥SB,DI⊥SC
c)CB⊥(SAC)
và các mặt bên hình chóp là các tam giác vuông
Cho A,B,C là ba góc của một tam giác. Chứng minh rằng:
\(\sin A+\sin B-\frac{\sqrt{2}}{2}\cos C\le\sqrt{2}\)
Cho tam giác ABC nội tiếp đường tròn (O). Đường trung trực của đoạn OA cắt đường thẳng BC tại X. Chứng minh rằng \(\dfrac{\overline{XB}}{\overline{XC}}=\dfrac{BO^2-BA^2}{CO^2-CA^2}\). Từ đó áp dụng chứng minh bài toán sau:
Cho tam giác ABC nội tiếp (O). Gọi A' đối xứng với A qua BC. B', C' xác định tương tự. Gọi O' là tâm của (A'B'C'). CMR (OAA'), (OBB'), (OCC') cùng đi qua 1 điểm khác O và điểm đó thuộc OO'.
Giải giúp mình bài tập này với. Xin chân thành cảm ơn! Cho tam giác ABC. Dựng bên ngoài ABC tam giác ABD và ACE vuông cân tại B và C. Gọi M là trung điểm DE. Dùng phép biến hình chứng minh tam giác MBC vuông cân. ( Cac ban oi dung phep bien hinh nhe!)
Cho hình chóp S.ABCD có đáy là hình thang ABCD, đáy lớn là AD và AD = 2BC. Gọi O là giao điểm của AC và BD, G là trọng tâm của tam giác SCD.
a) Chứng minh rằng OG // (SBC)
b) Cho M là trung điểm của SD. Chứng minh rằng CM // (SAB).
c) Giả sử điểm I nằm trong đoạn SC sao cho SC = 3SI/2. Chứng minh rằng SA // (BID).
Tìm giá trị tham số m để đồ thị hàm số y = x 4 - 2 ( m + 1 ) x 2 + 2 m + 3 có ba điểm cực trị A,B ,C sao cho trục hoành chia tam giác ABC thành một tam giác và một hình thang biết rằng tỉ số diện tích tam giác nhỏ được chia ra và diện tích tam giác ABC bằng 4 9