Dựa vào tam giác Pa-xcan:C14 = 4; C24 = 6
C25 = C14 + C24 = 4 + 6 = 10
Mà: 1 + 2 + 3 + 4 = 10
⇒ 1 + 2 + 3 + 4 = C25
Dựa vào tam giác Pa-xcan:C14 = 4; C24 = 6
C25 = C14 + C24 = 4 + 6 = 10
Mà: 1 + 2 + 3 + 4 = 10
⇒ 1 + 2 + 3 + 4 = C25
Dùng tam giác Pa-xcan, chứng tỏ rằng: 1 + 2 + … + 7 = C 8 2
cho a,b,c là 3 cạnh của 1 tam giác có chu vi bằng 4. chứng minh rằng: \(a^2+b^2+c^2+abc< 8\)
cho a,b,c là 3 cạnh của 1 tam giác có chu vi bằng 4. chứng minh rằng \(a^2+b^2+c^2+abc< 8\)
Chứng minh rằng các phương trình sau luôn có nghiệm: a)x^5 - 3x+3=0 b)x^5+x-1=0 c)x^4+x^3-3x^2+x+1=0
Trong hệ tọa độ Oxy cho tam giác ABC có A(3 ; 5) ; B( 1 ;2) và C( 5 ;2). Tìm tọa độ trọng tâm G của tam giác ABC ?
A. G( -9 ; -9)
B. 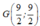
C. G( 3 ;3)
D.G(9 ; 9)
Cho A,B,C là ba góc của một tam giác. Chứng minh rằng:
\(\sin A+\sin B-\frac{\sqrt{2}}{2}\cos C\le\sqrt{2}\)
Cho tam giác ABC nội tiếp đường tròn (O). Đường trung trực của đoạn OA cắt đường thẳng BC tại X. Chứng minh rằng \(\dfrac{\overline{XB}}{\overline{XC}}=\dfrac{BO^2-BA^2}{CO^2-CA^2}\). Từ đó áp dụng chứng minh bài toán sau:
Cho tam giác ABC nội tiếp (O). Gọi A' đối xứng với A qua BC. B', C' xác định tương tự. Gọi O' là tâm của (A'B'C'). CMR (OAA'), (OBB'), (OCC') cùng đi qua 1 điểm khác O và điểm đó thuộc OO'.
Tìm giá trị tham số m để đồ thị hàm số y = x 4 - 2 ( m + 1 ) x 2 + 2 m + 3 có ba điểm cực trị A,B ,C sao cho trục hoành chia tam giác ABC thành một tam giác và một hình thang biết rằng tỉ số diện tích tam giác nhỏ được chia ra và diện tích tam giác ABC bằng 4 9
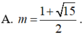
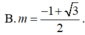
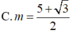
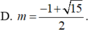
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , SA![]() (ABC) . Kẻ AH , AK lần lượt vuông góc với SB , SC tại H và K , có SA = AB = a .
(ABC) . Kẻ AH , AK lần lượt vuông góc với SB , SC tại H và K , có SA = AB = a .
1) Chứng minh tam giác SBC vuông .
2) Chứng minh tam giác AHK vuông và tính diện tích tam giác AHK .
3) Tính góc giữa AK và (SBC) .