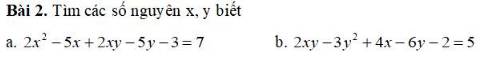a) \(2x^2-5x+2xy-5x-3=7\)
\(\left(2x^2+2xy\right)-\left(5x+5y\right)=7+3\)
\(2x\left(x+y\right)-5\left(x+y\right)=10\)
\(\left(x+y\right)\left(2x-5\right)=10\)
\(\Rightarrow2x-5\inƯ\left(10\right)=\left\{-10;-5;-2;-1;1;2;5;10\right\}\)
Mà \(x\in Z\)
\(\Rightarrow2x-5\) là số nguyên lẻ
\(\Rightarrow2x-5\in\left\{-5;-1;1;5\right\}\)
\(\Rightarrow2x\in\left\{0;4;6;10\right\}\)
\(\Rightarrow x\in\left\{0;2;3;5\right\}\)
*) \(x=0\)
\(\Rightarrow\left(0+y\right)\left(2.0-5\right)=10\)
\(\Rightarrow y.\left(-5\right)=10\)
\(\Rightarrow y=10:\left(-5\right)\)
\(\Rightarrow y=-2\)
*) \(x=2\Rightarrow\left(2+y\right)\left(2.2-5\right)=10\)
\(\Rightarrow\left(2+y\right).\left(-1\right)=10\)
\(\Rightarrow2+y=-10\)
\(\Rightarrow y=-10-2\)
\(\Rightarrow y=-12\)
*) \(x=3\Rightarrow\left(3+y\right)\left(2.3-5\right)=10\)
\(\Rightarrow3+y=10\)
\(\Rightarrow y=10-3\)
\(\Rightarrow y=7\)
*) \(x=5\Rightarrow\left(5+y\right)\left(2.5-5\right)=10\)
\(\Rightarrow\left(5+y\right).5=10\)
\(\Rightarrow5+y=10:5\)
\(\Rightarrow5+y=2\)
\(\Rightarrow y=2-5\)
\(\Rightarrow y=-3\)
Vậy ta tìm được các cặp giá trị \(\left(x;y\right)\) thỏa mãn:
\(\left(5;-3\right);\left(0;-2\right);\left(2;-12\right);\left(3;7\right)\)
b) \(2xy-3y^2+4x-6y-2=5\)
\(\left(2xy-3y^2\right)+\left(4x-6y\right)=5+2\)
\(y\left(2x-3y\right)+2\left(2x-3y\right)=7\)
\(\left(2x-3y\right)\left(y+2\right)=7\)
Bảng giá trị:
| y+2 | -7 | -1 | 1 | 7 |
| 2x-3y | -1 | -7 | 7 | 1 |
| y | -9 | -3 | -1 | 5 |
| x | -14 | -8 | 2 | 8 |
Vậy ta tìm được các cặp giá trị \(\left(x;y\right)\) thỏa mãn:
\(\left(-14;-9\right);\left(-8;-3\right);\left(2;-1\right);\left(8;5\right)\)