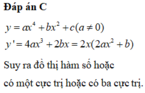Các câu hỏi tương tự
Cho các số thực a, b, c, d thỏa mãn 0 a b c d và hàm số y f(x). Biết hàm số y f(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y f(x) trên
[
0
;
d
]
. Khẳng định nào sau đây là khẳng định đúng? A. M + m f(b) + f(a) B. M + m f(d) + f(c) C. M + m f(0) + f(c) D. M + m f(0) + f(a)
Đọc tiếp
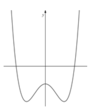
Cho các số thực a, b, c, d thỏa mãn 0 < a < b < c < d và hàm số y = f(x). Biết hàm số y = f'(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y = f(x) trên [ 0 ; d ] . Khẳng định nào sau đây là khẳng định đúng?

A. M + m = f(b) + f(a)
B. M + m = f(d) + f(c)
C. M + m = f(0) + f(c)
D. M + m = f(0) + f(a)
Cho hàm số
y
f
(
x
)
liên tục trên đoạn [a;b] có đồ thị như hình bên và
c
∈
a
;
b
. Gọi S là diện tích của hình phẳng (H) giới hạn bởi đồ thị hàm số
y
f
(
x
)
và các đường thẳng
y
0
,
x
a...
Đọc tiếp
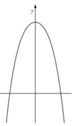
Cho hàm số y = f ( x ) liên tục trên đoạn [a;b] có đồ thị như hình bên và c ∈ a ; b . Gọi S là diện tích của hình phẳng (H) giới hạn bởi đồ thị hàm số y = f ( x ) và các đường thẳng y = 0 , x = a , x = b . . Mệnh đề nào sau đây sai?
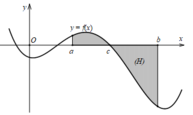
A. S = ∫ a c f x d x + ∫ c b f x d x
B. S = ∫ a c f x d x − ∫ c b f x d x
C. S = ∫ a b f x d x
D. S = ∫ a c f x d x + ∫ b c f x d x
Cho a là số thực tùy ý và b, c là các số thực dương khác 1.Hình vẽ bên là đồ thị của ba hàm số
y
x
a
,
y
log
b
x
,
y
log
c
x
,
x
0
. Khẳng định nào sau đây đúng? A.
a
c...
Đọc tiếp
Cho a là số thực tùy ý và b, c là các số thực dương khác 1.Hình vẽ bên là đồ thị của ba hàm số
y = x a , y = log b x , y = log c x , x > 0 .

Khẳng định nào sau đây đúng?
A. a < c < b
B. a > c > b
C. a > b > c
D. a < b < c
Cho a là số thực tùy ý và b, c là các số thực dương khác 1. Hình vẽ bên là đồ thị của ba hàm số
y
x
a
,
y
log
b
x
,
y
log
c
x
,
x
0
Khẳng định nào sau đây đúng A. acb B. acb C. abc D. abc
Đọc tiếp
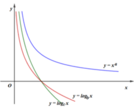
Cho a là số thực tùy ý và b, c là các số thực dương khác 1.
Hình vẽ bên là đồ thị của ba hàm số y = x a , y = log b x , y = log c x , x > 0
Khẳng định nào sau đây đúng
A. a<c<b
B. a<c<b
C. a>b>c
D. a<b<c
Cho hàm số
y
f
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
(a;b;c;d
∈
R, a
≠...
Đọc tiếp
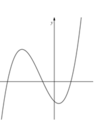
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d (a;b;c;d ∈ R, a ≠ 0) có đồ thị (C). Biết rằng đồ thị (C) đi qua gốc tọa độ và có đồ thị hàm số y = f’(x) cho bởi hình vẽ sau đây.

Tính giá trị H = f(4) – f(2)
A. H = 51
B. H = 54
C. H = 58
D. H = 64
Các đường cong ở hình bên là đồ thị của hàm số
y
a
x
+
b
c
x
+
d
với a,b,c,d là các số thực. Mệnh đề nào sau đây đúng? A.
y
0
,
∀
x
≠
2
B.
y...
Đọc tiếp
Các đường cong ở hình bên là đồ thị của hàm số y = a x + b c x + d với a,b,c,d là các số thực. Mệnh đề nào sau đây đúng?
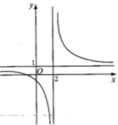
A. y ' < 0 , ∀ x ≠ 2
B. y ' < 0 , ∀ x ≠ 1
C. y ' > 0 , ∀ x ≠ 2
D. y ' > 0 , ∀ x ≠ 1
Đường cong của hình vẽ bên là đồ thị của hàm số
y
a
x
+
b
c
x
+
d
với a, b, c, d là các số thực. Mệnh đề nào sau đây là đúng A.
y
0
,
∀
x
≠
1
B.
y...
Đọc tiếp
Đường cong của hình vẽ bên là đồ thị của hàm số y = a x + b c x + d với a, b, c, d là các số thực. Mệnh đề nào sau đây là đúng

A. y ' > 0 , ∀ x ≠ 1
B. y ' > 0 , ∀ x ≠ 2
C. y ' < 0 , ∀ x ≠ 1
D. y ' < 0 , ∀ x ≠ 2
Biết đồ thị (C) ở hình bên là đồ thị hàm số
y
a
x
a
0
,
a
≠
1
.
Gọi (C’) là đường đối xứng với (C) qua đường thẳng yxHỏi (C’) là đồ thị của hàm số nào dưới đây? A.
y
log
1
2
x...
Đọc tiếp
Biết đồ thị (C) ở hình bên là đồ thị hàm số y = a x a > 0 , a ≠ 1 . Gọi (C’) là đường đối xứng với (C) qua đường thẳng y=x
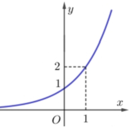
Hỏi (C’) là đồ thị của hàm số nào dưới đây?
A. y = log 1 2 x .
B. y = 2 x .
C. y = 1 2 x .
D. y = log 2 x .
Cho hàm số
y
f
x
a
x
3
+
b
x
2
+
c
x
+
d
a
,
b
,
c
∈
ℝ
,
a
≠
0
có đồ thị (C). Biết...
Đọc tiếp
Cho hàm số
y
=
f
x
=
a
x
3
+
b
x
2
+
c
x
+
d
a
,
b
,
c
∈
ℝ
,
a
≠
0
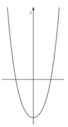
có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y = 4 tại điểm có hoành độ âm và đồ thị của hàm số y = f '(x) cho bởi hình vẽ dưới đây.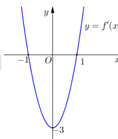 Tính diện tích S của hình phẳng giới hạn bởi đồ thị (C) và trục hoành.
Tính diện tích S của hình phẳng giới hạn bởi đồ thị (C) và trục hoành.
A. S = 9
B. S = 5 4
C. S = 21 4
D. S = 27 4