Các câu hỏi tương tự
Cho hàm số yf(x) có đạo hàm trên R. Đường cong trong hình vẽ bên là đồ thị của hàm số yf’(x),(yf’(x) liên tục trên R). Xét hàm số
g
x
f
x
2
-
2
. Mệnh đề nào dưới đây sai? A. Hàm số g(x) nghịch biến trên (-∞;-2). B. Hàm số g(x) đồng biến trên (2;+∞). C. Hàm số g(x)nghịch biến trên(-1;0). D. Hàm số g(x) ngh...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm trên R. Đường cong trong hình vẽ bên là đồ thị của hàm số y=f’(x),(y=f’(x) liên tục trên R). Xét hàm số g x = f x 2 - 2 . Mệnh đề nào dưới đây sai?
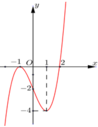
A. Hàm số g(x) nghịch biến trên (-∞;-2).
B. Hàm số g(x) đồng biến trên (2;+∞).
C. Hàm số g(x)nghịch biến trên(-1;0).
D. Hàm số g(x) nghịch biến trên (0;2).
Cho hàm số yf(x) có đồ thị như hình vẽ bên. Biết rằng yf(x) là một trong bốn hàm được đưa ra trong các phương án dưới đây. Tìm yf(x) A.
f
x
−
x
4
+
2
x
2
B.
f
x
−
x
4
+
2
x...
Đọc tiếp
Cho hàm số y=f(x) có đồ thị như hình vẽ bên. Biết rằng y=f(x) là một trong bốn hàm được đưa ra trong các phương án dưới đây. Tìm y=f(x)
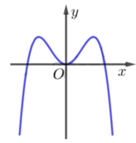
A. f x = − x 4 + 2 x 2
B. f x = − x 4 + 2 x 2 − 1
C. f x = x 4 + 2 x 2
D. f x = x 4 − 2 x 2
Số đường tiệm cận của đồ thị hàm số
y
x
2
−
2
+
x
2
−
4
x
2
−
4
x
+
3
là A. 0...
Đọc tiếp
Số đường tiệm cận của đồ thị hàm số y = x 2 − 2 + x 2 − 4 x 2 − 4 x + 3 là
A. 0
B. 2
C. 3
D. 1
1. Cho hàm số y2x-1/x-1 . Lấy M thuộc C với XMm . tiếp tuyến của C tại M cắt 2 đường tiệm cận tại A,B . Gọi I là giao của 2 đường tiệm cận . CMR : M là trung điểm của AB và tam giác IAB có diện tích không phụ thuộc vào M 2.cho yx+2/x-3 tìm M thuộc C sao cho khoảng cách từ M đến 2 đường tiệm cận C bằng nhau 3. cho y x+2/x-2 tìm M thuộc C sao cho M cách đều hai trục tọa độ . viết pttt của C biết tiếp tuyến đó đi qua A(-6;5) 4 . cho y x+1/x-1 . CMR (d) : 2x-y+m0 luôn cắt C tại A,B trên 2 nhánh củ...
Đọc tiếp
1. Cho hàm số y=2x-1/x-1 . Lấy M thuộc C với XM=m . tiếp tuyến của C tại M cắt 2 đường tiệm cận tại A,B . Gọi I là giao của 2 đường tiệm cận . CMR : M là trung điểm của AB và tam giác IAB có diện tích không phụ thuộc vào M
2.cho y=x+2/x-3 tìm M thuộc C sao cho khoảng cách từ M đến 2 đường tiệm cận C bằng nhau
3. cho y = x+2/x-2 tìm M thuộc C sao cho M cách đều hai trục tọa độ . viết pttt của C biết tiếp tuyến đó đi qua A(-6;5)
4 . cho y = x+1/x-1 . CMR (d) : 2x-y+m=0 luôn cắt C tại A,B trên 2 nhánh của (C) . tìm m để AB ngắn nhất
Cho hàm số y = x 2 + x + 2 x - 2 có đồ thị (C). Số tiệm cận của đồ thị (C) là:
A. 2
B. 0
C. 3
D. 1
Xét các mệnh đề sau(1). Đồ thị hàm số
y
1
2
x
-
3
có hai đường tiệm cận đứng và một đường tiệm cận ngang(2). Đồ thị hàm số
y
x
+
x
2
+
x
+
1...
Đọc tiếp
Xét các mệnh đề sau
(1). Đồ thị hàm số y = 1 2 x - 3 có hai đường tiệm cận đứng và một đường tiệm cận ngang
(2). Đồ thị hàm số y = x + x 2 + x + 1 x có hai đường tiệm cận ngang và một đường tiệm cận đứng
(3). Đồ thị hàm số y = x - 2 x - 1 x 2 - 1 có một đường tiệm cận ngang và hai đường tiệm cận đứng.
Số mệnh đề đúng là:
A. 0
B. 3
C. 2
D. 1
Cho hàm số yf(x) có đạo hàm
f
(
x
)
x
2
(
x
2
-
4
)
,
x
∈
R
. Mệnh đề nào sau đây là đúng? A. Hàm số đã cho có 2 điểm cực trị. B. Hàm số đã cho đạt cực đại tại x 2 C. Hàm số đã cho có 3 điểm cực trị. D. Hàm số đã cho đạt cực tiểu tại x -2
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = x 2 ( x 2 - 4 ) , x ∈ R . Mệnh đề nào sau đây là đúng?
A. Hàm số đã cho có 2 điểm cực trị.
B. Hàm số đã cho đạt cực đại tại x = 2
C. Hàm số đã cho có 3 điểm cực trị.
D. Hàm số đã cho đạt cực tiểu tại x = -2
Cho hàm số
y
x
−
1
x
−
3
. Xét các mệnh đề sau:(1) Hàm số nghịch biến trên
D
ℝ
3
(2) Đồ thị hàm số có một tiệm cận đứng là x1, tiệm cận ngang là y3.(3) Hàm số đã cho không có cực trị(4) Đồ thị hàm số nhận giao điểm I(3;1) của hai đường tiệm cận làm tâm đối xứng...
Đọc tiếp
Cho hàm số y = x − 1 x − 3 . Xét các mệnh đề sau:
(1) Hàm số nghịch biến trên D = ℝ \ 3
(2) Đồ thị hàm số có một tiệm cận đứng là x=1, tiệm cận ngang là y=3.
(3) Hàm số đã cho không có cực trị
(4) Đồ thị hàm số nhận giao điểm I(3;1) của hai đường tiệm cận làm tâm đối xứng.
Chọn các mệnh đề đúng ?
A. (1), (3), (4)
B. (3), (4)
C. (2), (3), (4)
D. (1), (4)
Cho hàm số
y
l
o
g
a
x
v
à
y
l
o
g
b
x
có đồ thị như hình vẽ bên. Đường thẳng x7 cắt trục hoành, đồ thị hàm số
y
l
o
g
a
x
và
y
l
o
g...
Đọc tiếp
Cho hàm số y = l o g a x v à y = l o g b x có đồ thị như hình vẽ bên. Đường thẳng x=7 cắt trục hoành, đồ thị hàm số y = l o g a x và y = l o g b x lần lượt tại H, M và N. Biết rằng HM=MN. Mệnh đề nào sau đây là đúng?
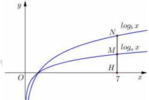
A. a = 7b
B. a = b 2
C. a = b 7
D. a = 2b




