Các câu hỏi tương tự
Người ta xây dựng một cái tháp gồm 11 tầng. Diện tích bề mặt của mỗi tầng bằng nửa diện tích bề mặt của tầng ngay bên dưới và diện tích bề mặt của tầng một bằng
3
4
diện tích đế tháp. Biết đế tháp có diện tích bằng 12288
m
2
. Diện tích bề mặt của tầng trên cùng là A. 4,5
m
2
B. 18
m
2
C. 9
m
2...
Đọc tiếp
Người ta xây dựng một cái tháp gồm 11 tầng. Diện tích bề mặt của mỗi tầng bằng nửa diện tích bề mặt của tầng ngay bên dưới và diện tích bề mặt của tầng một bằng 3 4 diện tích đế tháp. Biết đế tháp có diện tích bằng 12288 m 2 . Diện tích bề mặt của tầng trên cùng là
A. 4,5 m 2
B. 18 m 2
C. 9 m 2
D. 16 m 2
Cho hình chóp S.ABC có SA SB SC 1. Gọi G là trọng tâm của tứ diện. Xét mặt phẳng (α) thay đổi đi qua điểm G và cắt các cạnh SA, SB, SC lần lượt tại D, E, F. Giá trị lớn nhất của biểu thức
P
1
S
D
.
S
E
+
1
S
E
.
S
F
+...
Đọc tiếp
Cho hình chóp S.ABC có SA = SB = SC = 1. Gọi G là trọng tâm của tứ diện. Xét mặt phẳng (α) thay đổi đi qua điểm G và cắt các cạnh SA, SB, SC lần lượt tại D, E, F. Giá trị lớn nhất của biểu thức P = 1 S D . S E + 1 S E . S F + 1 S F . S D bằng
A. 16 3
B. 27 4
C. 16 9
D. 9 4
Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nửa diện tích của mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng bằng nửa diện tích của đế tháp (có diện tích là
12288
m
2
). Diện tích mặt trên cùng (tầng thứ 11) bằng A. 6
m
2
B. 8
m
2
C. 10
m
2
D. 12...
Đọc tiếp
Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nửa diện tích của mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng bằng nửa diện tích của đế tháp (có diện tích là 12288 m 2 ). Diện tích mặt trên cùng (tầng thứ 11) bằng
A. 6 m 2
B. 8 m 2
C. 10 m 2
D. 12 m 2
Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nữadiện tích của mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa diện tích của đế tháp (có diện tích là
12288
m
2
). Tính diện tích mặt trên cùng? A.
8
m
2
B.
6
m
2
C.
10
m...
Đọc tiếp
Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nữadiện tích của mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa diện tích của đế tháp (có diện tích là 12288 m 2 ). Tính diện tích mặt trên cùng?
A. 8 m 2
B. 6 m 2
C. 10 m 2
D. 12 m 2
Người ta thiết kế một thùng chứa hình trụ (như hình vẽ) có thể tích V không đổi. Biết rằng giá của vật liệu làm mặt đáy và nắp của thùng bằng nhau và đắt gấp 3 lần so với giá vật liệu để làm mặt xung quanh của thùng (chi phí cho mỗi đơn vị diện tích). Gọi chiều cao của thùng là h và bán kính đáy là r . Tính tỷ số
h
r
sao cho chi phí vật liệu sản xuất thùng nhỏ nhất. A.
h
r
1 B.
h...
Đọc tiếp
Người ta thiết kế một thùng chứa hình trụ (như hình vẽ) có thể tích V không đổi. Biết rằng giá của vật liệu làm mặt đáy và nắp của thùng bằng nhau và đắt gấp 3 lần so với giá vật liệu để làm mặt xung quanh của thùng (chi phí cho mỗi đơn vị diện tích). Gọi chiều cao của thùng là h và bán kính đáy là r . Tính tỷ số h r sao cho chi phí vật liệu sản xuất thùng nhỏ nhất.
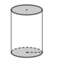
A. h r = 1
B. h r = 2
C. h r = 6
D. h r = 9
Trong không gian Oxyz, cho mặt cầu (S1) có tâm I1(2;1;0), bán kính R1 3; mặt cầu (S2) có tâm I2(0;1;0), bán kính R2 2. Đường thẳng d thay đổi nhưng luôn tiếp xúc với cả hai mặt cầu (S1),(S2). Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của khoảng cách từ điểm A(1;1;1) đến đường thẳng d. Giá trị của M.m bằng A.5,5 B. 4,5 C. 6,5 D. 7,5
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S1) có tâm I1(2;1;0), bán kính R1 = 3; mặt cầu (S2) có tâm I2(0;1;0), bán kính R2 = 2. Đường thẳng d thay đổi nhưng luôn tiếp xúc với cả hai mặt cầu (S1),(S2). Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của khoảng cách từ điểm A(1;1;1) đến đường thẳng d. Giá trị của M.m bằng
A.5,5
B. 4,5
C. 6,5
D. 7,5
Trong không gian Oxyz, cho mặt cầu
S
1
có tâm I(2;1;1) có bán kính bằng 4 và mặt cầu
S
2
có tâm J(2;1;5) có bán kính bằng 2. (P) là mặt phẳng thay đổi tiếp xúc với hai mặt cầu
S
1
S
2
. Đặt M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của khoảng cách từ điểm O...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu S 1 có tâm I(2;1;1) có bán kính bằng 4 và mặt cầu S 2 có tâm J(2;1;5) có bán kính bằng 2. (P) là mặt phẳng thay đổi tiếp xúc với hai mặt cầu S 1 S 2 . Đặt M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của khoảng cách từ điểm O đến (P). Giá trị M+m bằng?
A. 8 3
B. 9
C. 8
D. 15
Cho mặt cầu
S
có bán kính
R
5
c
m
. Mặt phẳng
P
cắt mặt cầu
S
theo giao tuyến là đường tròn
C
có chu vi bằng
8
π
. Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn
C
, điểm D thuộc
S
(D không thuộc đường tròn
C
) và tam giác ABC là...
Đọc tiếp
Cho mặt cầu S có bán kính R = 5 c m . Mặt phẳng P cắt mặt cầu S theo giao tuyến là đường tròn C có chu vi bằng 8 π . Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn C , điểm D thuộc S (D không thuộc đường tròn C ) và tam giác ABC là tam giác đều. Tính thể tích lớn nhất của tứ diện ABCD.
A. 32 3 c m 3
B. 60 3 c m 3
C. 20 3 c m 3
D. 96 3 c m 3
Trong không gian Oxyz, cho mặt cầu
S
1
có tâm
I
2
;
1
;
1
bán kính bằng 4 và mặt cầu
S
2
có tâm
...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu S 1 có tâm I 2 ; 1 ; 1 bán kính bằng 4 và mặt cầu S 2 có tâm J 2 ; 1 ; 5 bán kính bằng 2. (P) là mặt phẳng thay đổi tiếp xúc với hai mặt cầu S 1 , S 2 . Đặt M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của khoảng cách từ O đến mặt phẳng Giá trị M + m bằng:
A. 8
B. 8 3 .
C. 9
D. 15 .



