Các câu hỏi tương tự
Hàm số bậc hai nào sau đây có đồ thị đi qua 3 điểm A(0;-2), B(1;2) ,C(-1;-4) ? A.
y
x
2
-
4
x
+
3
.
B.
y
-
2...
Đọc tiếp
Hàm số bậc hai nào sau đây có đồ thị đi qua 3 điểm A(0;-2), B(1;2) ,C(-1;-4) ?
A. y = x 2 - 4 x + 3 .
B. y = - 2 x 2 + 6 x - 2 .
C. y = - 3 x 2 + x - 2 .
D. y = x 2 + 3 x - 2 .
Cho hàm số
f
x
3
2
x
-
2
.
3
x
có đồ thị như hình vẽ sauCó bao nhiêu mệnh đề đúng trong các mệnh đề sau?(1) Đường thẳng y 0 cắt đồ thị hàm số (C) tại điểm có hoành độ là
x
log
3
2
(2) Bất phương trình
f
x
≥
-...
Đọc tiếp
Cho hàm số f x = 3 2 x - 2 . 3 x có đồ thị như hình vẽ sau
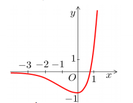
Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) Đường thẳng y = 0 cắt đồ thị hàm số (C) tại điểm có hoành độ là x = log 3 2
(2) Bất phương trình f x ≥ - 1 có nghiệm duy nhất.
(3) Bất phương trình f x ≥ 0 có tập nghiệm là - ∞ ; log 3 2
(4) Đường thẳng y = 0 cắt đồ thị hàm số (C) tại 2 điểm phân biệt.
A. 2
B. 4
C. 1
D. 3
Cho hàm số
f
x
3
2
x
−
2.3
x
có đồ thị như hình vẽ sauCó bao nhiêu mệnh đề đúng trong các mệnh đề sau?(1) Đường thẳng y0 cắt đồ thị hàm số (C) tại điểm có hoành độ là
x
log
3
2
(2) Bất phương trình
f
x
≥...
Đọc tiếp
Cho hàm số f x = 3 2 x − 2.3 x có đồ thị như hình vẽ sau
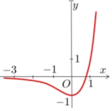
Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) Đường thẳng y=0 cắt đồ thị hàm số (C) tại điểm có hoành độ là
x
=
log
3
2
(2) Bất phương trình
f
x
≥
−
1
có nghiệm duy nhất.
(3) Bất phương trình
f
x
≥
0
có tập nghiệm là
−
∞
;
log
3
2
(4) Đường thẳng y=0 cát đồ thị hàm số (C) tại 2 điểm phân biệt
A. 2.
B. 4.
C. 1.
D. 3.
Cho hàm số
y
f
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
(a,b,cÎR, a≠0) có đồ thị (C). Biết đồ thị (C) đi qua A(1;4) và đồ thị hàm số
y
f
’
(
x
)
cho bởi hình vẽ. Giá trị
f
(
3
)
-
2...
Đọc tiếp
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d (a,b,cÎR, a≠0) có đồ thị (C). Biết đồ thị (C) đi qua A(1;4) và đồ thị hàm số y = f ’ ( x ) cho bởi hình vẽ. Giá trị f ( 3 ) - 2 f ( 1 ) là
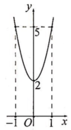
A. 30
B. 24
C. 26
D. 27
Cho hàm số y f(x) xác định trên
ℝ
và có đồ thị của hàm số
f
(
x
)
,
biết
f
(
3
)
+
f
(
2
)
f...
Đọc tiếp
Cho hàm số y = f(x) xác định trên ℝ và có đồ thị của hàm số f ' ( x ) , biết f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) và các khẳng định sau:
Hàm số y = f(x) có 2 điểm cực trị.
Hàm số y = f(x) đồng biến trên khoảng ( - ∞ ; 0 ) .
Max [ 0 ; 3 ] f ( x ) = f ( 3 ) .
Min ℝ f ( x ) = f ( 2 ) .
Max [ - ∞ ; 2 ] f ( x ) = f ( 0 ) .

Số khẳng định đúng là
A. 2.
B. 3.
C. 4.
C. 4.
Gọi (C) là đồ thị hàm số
y
x
-
7
x
+
1
, A, B là các điểm thuộc (C) có hoành độ lần lượt là 0 và 3. M là điểm thay đổi trên (C) sao cho
0
x
M
3
, tìm giá trị lớn nhất của diện tích
∆
A
B
M
A. 3 B. 5 C. 6 D....
Đọc tiếp
Gọi (C) là đồ thị hàm số y = x - 7 x + 1 , A, B là các điểm thuộc (C) có hoành độ lần lượt là 0 và 3. M là điểm thay đổi trên (C) sao cho 0 < x M < 3 , tìm giá trị lớn nhất của diện tích ∆ A B M
A. 3
B. 5
C. 6
D. 3 5
Gọi (C) là đồ thị hàm số
y
x
-
7
x
+
1
, A, B là các điểm thuộc (C) có hoành độ lần lượt là 0 và 3. M là điểm thay đổi trên (C) sao cho 0xM3, tìm giá trị lớn nhất của diện tích
∆
A
M
B
A. 3 B. 5 C. 5 D. 3
5
Đọc tiếp
Gọi (C) là đồ thị hàm số y = x - 7 x + 1 , A, B là các điểm thuộc (C) có hoành độ lần lượt là 0 và 3. M là điểm thay đổi trên (C) sao cho 0<xM<3, tìm giá trị lớn nhất của diện tích ∆ A M B
A. 3
B. 5
C. 5
D. 3 5
Cho hàm số
y
x
3
−
m
x
2
+
3
x
+
1
và
M
1
;
−
2
.
Biết có 2 giá trị của m là
m
1
và
m
2
để đường thẳng
Δ
:
y...
Đọc tiếp
Cho hàm số y = x 3 − m x 2 + 3 x + 1 và M 1 ; − 2 . Biết có 2 giá trị của m là m 1 và m 2 để đường thẳng Δ : y = x + 1 cắt đồ thị tại 3 điểm phân biệt A 0 ; 1 , B, C sao cho Δ M B C có diện tích bằng 4 2 . Hỏi m 1 2 + m 2 2 thuộc khoảng nào trong các khoảng nào sau đây
A. 15 ; 17
B. 3 ; 5
C. 31 ; 33
D. 16 ; 18
Cho hàm số
y
x
−
3
x
+
1
(C) và điểm
M
a
;
b
thuộc đồ thị (C). Đặt
T
3
(
a
+
b
)
+
2
a
b
, khi đó để tổng khoảng cách từ điểm M đến hai trục toạ đ...
Đọc tiếp
Cho hàm số y = x − 3 x + 1 (C) và điểm M a ; b thuộc đồ thị (C). Đặt T = 3 ( a + b ) + 2 a b , khi đó để tổng khoảng cách từ điểm M đến hai trục toạ độ là nhỏ nhất thì mệnh đề nào sau đây là đúng?
A. − 3 < T < − 1.
B. − 1 < T < 1.
C. 1 < T < 3.
Cho hàm số yf(x) xác định trên
ℝ
và có đồ thị của hàm số f(x), biết f(3)+f(20f(0)+f(1) và các khẳng định sau:1) Hàm số yf(x) có 2 điểm cực trị2) Hàm số yf(x) đồng biến trên khoảng
-
∞
;
0
3)
M
a
x
0
;
3
f...
Đọc tiếp
Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f'(x), biết f(3)+f(20=f(0)+f(1) và các khẳng định sau:
1) Hàm số y=f(x) có 2 điểm cực trị
2) Hàm số y=f(x) đồng biến trên khoảng - ∞ ; 0
3) M a x 0 ; 3 f x = f 3
4) M a x ℝ f x = f 2
5) M a x - ∞ ; 2 f x = f 0 .
Số khẳng định đúng là

A. 2
B. 3
C. 4
D. 5



