Các câu hỏi tương tự
Đặt log 3 p và log 5 q Hãy biểu diễn log1530 theo p và q A. B. C. D.
Đọc tiếp
Đặt log 3= p và log 5= q Hãy biểu diễn log1530 theo p và q
A. 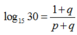
B. 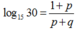
C. 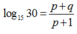
D. 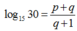
Cho log a 10; log b 100. Khi đó bằng A. 290 B. 310 C. –290 D. 30
Đọc tiếp
Cho log a= 10; log b = 100. Khi đó ![]() bằng
bằng
A. 290
B. 310
C. –290
D. 30
log3(3+sqrt{3}) log4xLeftrightarrowlog3(3+sqrt{3}) log3x : log34Leftrightarrowlog3(3+sqrt{3}).log34 log3xLeftrightarrowlog3(left(3+sqrt{3}right)^{log_{ }_34} log3xLeftrightarrowx left(3+sqrt{3}right)^{log_34}ko có đt nên tớ làm trong này
Đọc tiếp
log3(\(3+\sqrt{3}\)) > log4x
\(\Leftrightarrow\)log3(\(3+\sqrt{3}\)) > log3x : log34
\(\Leftrightarrow\)log3(\(3+\sqrt{3}\)).log34 > log3x
\(\Leftrightarrow\)log3(\(\left(3+\sqrt{3}\right)^{log_{ }_34}\)> log3x
\(\Leftrightarrow\)x < \(\left(3+\sqrt{3}\right)^{log_34}\)
ko có đt nên tớ làm trong này
Tìm tập nghiệm của phương trình l o g ( x + 3 ) + l o g ( x - 1 ) = l o g ( x 2 - 2 x - 3 )
A. ∅
B. {0}
C. R
D. (1; +∞)
Cho a là số nguyên dương lớn nhất thỏa mãn \(3{\log _3}\left( {1 + \sqrt a + \sqrt[3]{a}} \right) > 2{\log _2}\sqrt a\).Tìm phần nguyên của \({\log _2}\left( {2017a} \right)\)
A.14
B.22
C.16
D.19
Đặt m log 2 và n log 7. Hãy biểu diễn
log
6125
7
theo m và n.
Đọc tiếp
Đặt m = log 2 và n = log 7. Hãy biểu diễn log 6125 7 theo m và n.
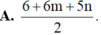
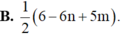
![]()
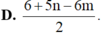
Cho x, y 0 thỏa mãn log(x + 2y) log x + log y. Khi đó, giá trị nhỏ nhất của biểu thức
P
x
2
1
+
2
y
+
4
y
2
1
+
x
là: A.
6
B. ...
Đọc tiếp
Cho x, y > 0 thỏa mãn log(x + 2y) = log x + log y. Khi đó, giá trị nhỏ nhất của biểu thức
P = x 2 1 + 2 y + 4 y 2 1 + x là:
A. 6
B. 32 5
C. 31 5
D. 29 5
Giá trị của của biểu thức
P
49
log
7
6
+
10
1
+
log
3
-
3
log
9
25
là A. P 61 B. P 35 C....
Đọc tiếp
Giá trị của của biểu thức P = 49 log 7 6 + 10 1 + log 3 - 3 log 9 25 là
A. P = 61
B. P = 35
C. P = 56
D. P = 65
Giải phương trình logx = log(x + 3) - log(x - 1)
A. x = 1
B. x = 3
C. x = 4
D. x = -1, x = 3
Tập nghiệm của bất phương trình log(x2 + 25) > log(10x) là
![]()
![]()
![]()
![]()







