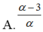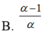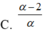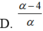Các câu hỏi tương tự
Cho log a 10; log b 100. Khi đó bằng A. 290 B. 310 C. –290 D. 30
Đọc tiếp
Cho log a= 10; log b = 100. Khi đó ![]() bằng
bằng
A. 290
B. 310
C. –290
D. 30
Đặt m log 2 và n log 7. Hãy biểu diễn
log
6125
7
theo m và n.
Đọc tiếp
Đặt m = log 2 và n = log 7. Hãy biểu diễn log 6125 7 theo m và n.
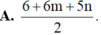
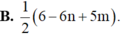
![]()
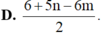
Đặt log 3 p và log 5 q Hãy biểu diễn log1530 theo p và q A. B. C. D.
Đọc tiếp
Đặt log 3= p và log 5= q Hãy biểu diễn log1530 theo p và q
A. 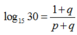
B. 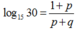
C. 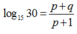
D. 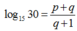
Cho x, y 0 thỏa mãn log(x + 2y) log x + log y. Khi đó, giá trị nhỏ nhất của biểu thức
P
x
2
1
+
2
y
+
4
y
2
1
+
x
là: A.
6
B. ...
Đọc tiếp
Cho x, y > 0 thỏa mãn log(x + 2y) = log x + log y. Khi đó, giá trị nhỏ nhất của biểu thức
P = x 2 1 + 2 y + 4 y 2 1 + x là:
A. 6
B. 32 5
C. 31 5
D. 29 5
Cho
f
x
a
ln
x
+
x
2
+
1
+
b
sin
x
+
6
với
a
,
b
∈
ℝ
. Biết rằng f(log(log e)) 2. Tính giá trị của f(log(ln10)). A. 10 B. 2 C. 4 D. 8
Đọc tiếp
Cho f x = a ln x + x 2 + 1 + b sin x + 6 với a , b ∈ ℝ . Biết rằng f(log(log e)) = 2. Tính giá trị của f(log(ln10)).
A. 10
B. 2
C. 4
D. 8
Tính giá trị biểu thức:
P
l
o
g
(
t
a
n
1
o
)
+
l
o
g
(
t
a
n
2
o
)
+
l
o
g
(
t
a
n
3
o
)
+
.
.
.
+
l
o
g
(
t
a
n
88
o
)
+
l...
Đọc tiếp
Tính giá trị biểu thức: P = l o g ( t a n 1 o ) + l o g ( t a n 2 o ) + l o g ( t a n 3 o ) + . . . + l o g ( t a n 88 o ) + l o g ( t a n 89 o )
A. 1
B. 0
C. 1 2 log 2
D. 1 2 log 3 2
Cho các số thực dương a,b thỏa mãn
log
a
x
,
log
b
y
. Tính
P
log
(
a
2
b
3
)
Đọc tiếp
Cho các số thực dương a,b thỏa mãn log a = x , log b = y . Tính P = log ( a 2 b 3 )
![]()
![]()
![]()
![]()
Cho a là số nguyên dương lớn nhất thỏa mãn \(3{\log _3}\left( {1 + \sqrt a + \sqrt[3]{a}} \right) > 2{\log _2}\sqrt a\).Tìm phần nguyên của \({\log _2}\left( {2017a} \right)\)
A.14
B.22
C.16
D.19
Tính giá trị của biểu thức
S
log
1
2
+
log
2
3
log
3
4
+
.
.
.
+
log
99
100
A.
1
10
B.
-
1
10
C. 2...
Đọc tiếp
Tính giá trị của biểu thức S = log 1 2 + log 2 3 = log 3 4 + . . . + log 99 100
A. 1 10
B. - 1 10
C. 2
D. -2
Tính giá trị của biểu thức
P
log
(
tan
1
0
)
+
log
(
tan
2
0
)
+
log
(
tan
3
0
)
+
.
.
.
+
log
(
tan
89
0
)
.
Đọc tiếp
Tính giá trị của biểu thức P = log ( tan 1 0 ) + log ( tan 2 0 ) + log ( tan 3 0 ) + . . . + log ( tan 89 0 ) .
![]()
![]()
![]()
![]()