- Đặt u = x 3 - 2 x 2 thì:

- Theo công thức tính đạo hàm của hàm số hợp, ta có:
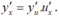
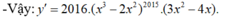
Chọn B.
- Đặt u = x 3 - 2 x 2 thì:

- Theo công thức tính đạo hàm của hàm số hợp, ta có:
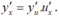
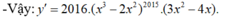
Chọn B.
Đạo hàm của hàm số \(y=\left(x^2-\dfrac{2}{x}\right)^3\)là:
A. \(y'=6\left(x+\dfrac{1}{x^2}\right)\left(x^2-\dfrac{2}{x}\right)^2\)
B. \(y'=3\left(x^2-\dfrac{2}{x}\right)^2\)
C. \(y'=6\left(x-\dfrac{1}{x^2}\right)\left(x^2-\dfrac{2}{x}\right)^2\)
D. \(y'=6\left(x-\dfrac{1}{x}\right)\left(x^2-\dfrac{2}{x}\right)^2\)
Cho khai triển: \(\left(1+x+x^2+...+x^{2015}\right)^{2016}=a_0+a_1x+a_2x^2+...+a_{4062240}x^{4062240}\). Tính giá trị biểu thức: \(T=C^0_{2016}a_{2016}-C^1_{2016}a^{2015}+C^2_{2016}a_{2014}-...+C^{2016}_{2016a_{ }0}\)
Đạo hàm của hàm số y = x 3 - x + 2016 bằng:
A. 3 x 2 - 1 x
B 3 x 2 + 1 2 x
C. 3 x 3 - 1 2 x
D. 3 x 2 - 1 2 x
tính đạo hàm của các hàm số sau
a) \(y=\dfrac{x^2+3x-1}{x+2}\)
b) \(y=\dfrac{2x^2-x}{x^2+1}\)
c) \(y=\dfrac{3-2x}{x-1}+\sqrt{2x-3}\)
1. đạo hàm của hàm số f(x) = 2x - 5 tại \(x_0=4\)
2. đạo hàm của hàm số \(y=x^2-3\sqrt{x}+\dfrac{1}{x}\)
3. đạo hàm của hàm số \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt{x}\) tại điểm x = 1
Tính đạo hàm của hàm số
1.\(y=\dfrac{1}{4}x^2-x+3\)
2.y=(sinx-1)(2x-3)
3.\(y=\sqrt{x^2-3x+1}\)
4.y \(=\dfrac{x-1}{x+3}\)
1) đạo hàm của hàm số \(y=x^2-3\sqrt{x}+\dfrac{1}{x}\)
2) đạo hàm của hàm số \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt{x}\) tại điểm x = 1
Đạo hàm của hàm số \(y=\left(-x^2+3x+7\right)^7\) là:
A. \(y'=7\left(-2x+3\right)\left(-x^2+3x+7\right)^6\)
B. \(y'=7\left(-x^2+3x+7\right)^6\)
C. \(y'=\left(-2x+3\right)\left(-x^2+3x+7\right)^6\)
D. \(y'=7\left(-2x+3\right)\left(-x^2+3x+7\right)^6\)
Tính các đạo hàm của hàm số sau:
a) \(y=\sqrt{x}\left(x+3\right)\)
b) \(y=\sqrt{2x^2-6x-9}\)
c) \(y=\left(\sqrt{x^2+1}+x\right)^{10}\)
tính đạo hàm của các hàm số sau
a) \(y=x^2+3x-6x^6+\dfrac{2x-3}{x-1}\)
b) \(y=3x^2-4x+\sqrt{2x^2-3x+1}\)
c) \(y=\sqrt{4x^2-3x+1}-4\)