a) \(A=\left(9x^2-6xy+4y^2+1\right)\left(3x+2y\right)-\left(3x^5y+\dfrac{8}{9}x^2y^4-x^3y\right):\left(\dfrac{1}{9}x^2y\right)\)
\(=3x\left(9x^2-6xy+4y^2+1\right)+2y\left(9x^2-6xy+4y^2+1\right)-\left(3x^5y:\dfrac{1}{9}x^2y+\dfrac{8}{9}x^2y^4:\dfrac{1}{9}x^2y-x^3y:\dfrac{1}{9}x^2y\right)\)\(=27x^3-18x^2y+12xy^2+3x+18x^2y-12xy^2+8y^3+2y-27x^3-8y^3+9x\)
\(=12x+2y\)
b) \(B=\left(5x^3y^2-4x^2y^3\right):2x^2y^2+\left(3x^4y+6xy^2\right):3xy-x\left(x^2-0,5\right)\)
\(=5x^3y^2:2x^2y^2-4x^2y^3:2x^2y^2+3x^4y:3xy+6xy^2:3xy-x^3+0,5x\)
\(=2,5x-2y+x^3+2y-x^3+0,5x\)
\(=2,5x+0,5x\)
\(=3x\)
c) \(C=\left[9x^3\left(x^2-1\right)-6x^2\left(x^2-1\right)^2+12x\left(x^2-1\right)\right]:3x\left(x^2-1\right)\)
\(=9x^3\left(x^2-1\right):3x\left(x^2-1\right)-6x^2\left(x^2-1\right)^2:3x\left(x^2-1\right)+12x\left(x^2-1\right):3x\left(x^2-1\right)\)
\(=9x^3:3x-6x^2\left(x^2-1\right):3x+12x:3x\)
\(=3x^2-2x\left(x^2-1\right)+4\)
\(=-2x^3+3x^2+2x+4\)
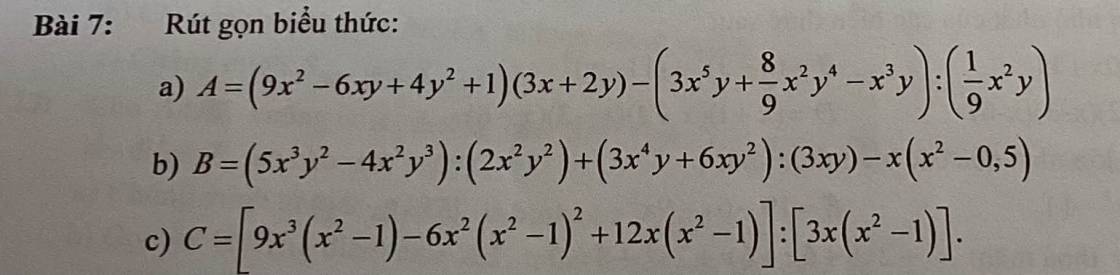
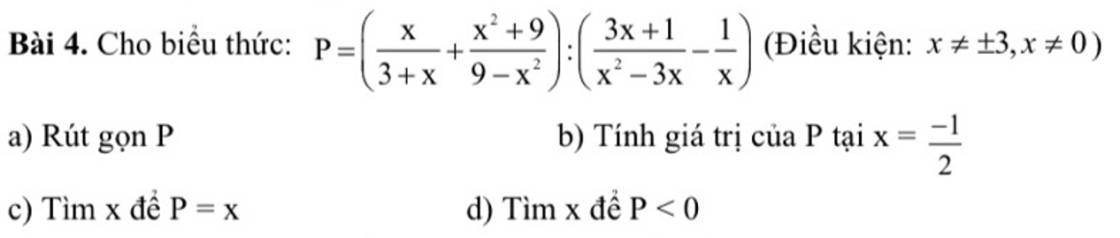
ai giúp mình phần 1 với ạ 
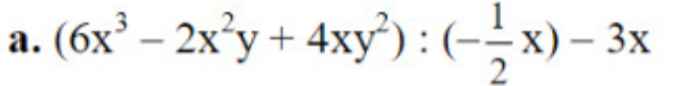Cứu với ạ sắp tới hạn nộp r,xin cảm ơn rất rất nhiều