có vẽ hình nhaaa
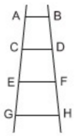
a: Xét ΔABC có \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\left(=\dfrac{1}{3}\right)\)
nên DE//BC
Xét ΔADE và ΔABC có
\(\widehat{ADE}=\widehat{ABC}\)(hai góc đồng vị, DE//BC)
\(\widehat{A}\) chung
Do đó: ΔADE đồng dạng với ΔABC
b: Xét tứ giác BDEF có
DE//BF
BD//EF
Do đó: BDEF là hình bình hành
Xét ΔCEF và ΔCAB có
\(\widehat{CEF}=\widehat{CAB}\)(hai góc đồng vị, EF//AB)
\(\widehat{C}\) chung
Do đó: ΔCEF đồng dạng với ΔCAB
mà ΔEAD đồng dạng với ΔCAB
nên ΔCEF~ΔEAD
c: Xét ΔABC có DE//BC
nên \(\dfrac{DE}{BC}=\dfrac{AD}{AB}\)
=>\(\dfrac{DE}{18}=\dfrac{1}{3}\)
=>\(DE=\dfrac{1}{3}\cdot18=6\left(cm\right)\)
mà DE=BF(BDEF là hình bình hành)
nên BF=6cm
Ta có: BF+FC=BC
=>FC+6=18
=>FC=12(cm)
