Các câu hỏi tương tự
Cho đa giác lồi (H) có 22 cạnh. Gọi X là tập hợp của các tam giác có 3 đỉnh là ba đỉnh của (H). Chọn ngẫu nhiên hai tam giác trong X. Tính xác suất để chọn được 1 tam giác có 1 cạnh là cạnh của đa giác (H) và 1 tam giác không có cạnh nào là cạnh của đa giác (H) (Kết quả làm tròn đến số thập phân thứ ba) A. 0,374. B. ,0375. C. 0,376. D. 0,377.
Đọc tiếp
Cho đa giác lồi (H) có 22 cạnh. Gọi X là tập hợp của các tam giác có 3 đỉnh là ba đỉnh của (H). Chọn ngẫu nhiên hai tam giác trong X. Tính xác suất để chọn được 1 tam giác có 1 cạnh là cạnh của đa giác (H) và 1 tam giác không có cạnh nào là cạnh của đa giác (H) (Kết quả làm tròn đến số thập phân thứ ba)
A. 0,374.
B. ,0375.
C. 0,376.
D. 0,377.
Cho lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a và có đường cao h. Gọi I là trung điểm của cạnh BC. Đường thẳng A’I cắt hình trụ nội tiếp nói trên theo một đoạn thẳng. Tính độ dài đoạn thẳng đó.
Cho hình chóp S.ABCD có đáy là hình thang.
A
D
/
/
B
C
,
A
D
2
B
C
2
a
. Gọi E, F lần lượt là trọng tâm các tam giác SAD và SBC. Gọi d là giao tuyến của hai mặt phẳng (EBC) và (FAD); M,N lần lượt là giao điểm của d với các mặt phẳng (SAB), (SCD). Độ dài đoạn thẳng MN bằng
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang. A D / / B C , A D = 2 B C = 2 a . Gọi E, F lần lượt là trọng tâm các tam giác SAD và SBC. Gọi d là giao tuyến của hai mặt phẳng (EBC) và (FAD); M,N lần lượt là giao điểm của d với các mặt phẳng (SAB), (SCD). Độ dài đoạn thẳng MN bằng
![]()
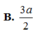
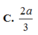
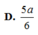
Cho H là đa giác đều 2n đỉnh nội tiếp đường tròn tâm O n ∈ N , n ≥ 2 . Gọi S là tập hợp các tam giác có ba đỉnh là các đỉnh của đa giác H . Chọn ngẫu nhiên một tam giác thuộc tập S, biết rằng xác suất chọn được một tam giác vuông trong tập S là 1 3. Tìm n.
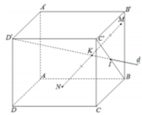
Cho hình lập phương ABCD.ABCD có cạnh bằng a. Một đường thẳng d đi qua đỉnh D¢ và tâm I của mặt bên BCCB. Hai điểm M, N thay đổi lần lượt thuộc các mặt phẳng (BCCB) và (ABCD) sao cho trung điểm K của MN thuộc đường thẳng d (tham khảo hình vẽ). Giá trị bé nhất của độ dài đoạn thẳng MN là
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Một đường thẳng d đi qua đỉnh D¢ và tâm I của mặt bên BCC'B'. Hai điểm M, N thay đổi lần lượt thuộc các mặt phẳng (BCC'B') và (ABCD) sao cho trung điểm K của MN thuộc đường thẳng d (tham khảo hình vẽ). Giá trị bé nhất của độ dài đoạn thẳng MN là
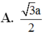
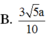
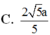
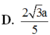
Cho đoạn thẳng AB cố định trong không gian và có độ dài AB 2. Qua các điểm A và B lần lượt kẻ các đường thẳng Ax và By chéo nhau thay đổi nhưng luôn vuông góc với đoạn thẳng AB. Trên các đường thẳng đó lần lượt lấy các điểm M N, sao cho AM+2BN3. Tìm giá trị lớn nhất của thể tích khối tứ diện ABMN ?
Đọc tiếp
Cho đoạn thẳng AB cố định trong không gian và có độ dài AB = 2. Qua các điểm A và B lần lượt kẻ các đường thẳng Ax và By chéo nhau thay đổi nhưng luôn vuông góc với đoạn thẳng AB. Trên các đường thẳng đó lần lượt lấy các điểm M N, sao cho AM+2BN=3. Tìm giá trị lớn nhất của thể tích khối tứ diện ABMN ?


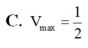
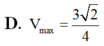
Cho a; b; c lần lượt là độ dài của hai cạnh góc vuông và cạnh huyền của một tam giác vuông, trong đó c - b và c + b khác 1. Khi đó logc+ba + logc-ba bằng: A.-2logc+ba.logc-ba. B. 3logc+ba.logc-ba. C.2logc+ba.logc-ba. D. Tất cả sai
Đọc tiếp
Cho a; b; c lần lượt là độ dài của hai cạnh góc vuông và cạnh huyền của một tam giác vuông, trong đó c - b và c + b khác 1. Khi đó logc+ba + logc-ba bằng:
A.-2logc+ba.logc-ba.
B. 3logc+ba.logc-ba.
C.2logc+ba.logc-ba.
D. Tất cả sai
Cho (C) là đồ thị của hàm số
y
x
-
3
x
+
1
Biết rằng chỉ có đúng hai điểm thuộc đồ thị (C) cách đều hai trục tọa độ. Gọi các điểm đó lần lượt là M và N. Tính độ dài đoạn thẳng MN. A. B. MN 3 C. D.
Đọc tiếp
Cho (C) là đồ thị của hàm số y = x - 3 x + 1 Biết rằng chỉ có đúng hai điểm thuộc đồ thị (C) cách đều hai trục tọa độ. Gọi các điểm đó lần lượt là M và N. Tính độ dài đoạn thẳng MN.
A.![]()
B. MN = 3
C. ![]()
D. ![]()
Một cái ao có hình ABCDE (như hình vẽ), ở giữa ao có một mảnh vườn hình tròn bán kính 10m, người ta muốn bắc một cây cầu từ bờ AB của ao đến vườn. Hỏi độ dài ngắn nhất l của cây cầu gần nhất với so nào dưới đây biết. - Hai bờ AE và BC nằm trên hai đường thẳng vuông góc với nhau, hai đường thẳng này cắt nhau tại điểm O; - Bờ AB là một phần của một parabol có đỉnh là điểm A và có trục đối xứng là đường thẳng OA ; - Độ dài đoạn OA và OB lần lượt là 40m và 20m; - Tâm I của mảnh vườn cách đường thẳn...
Đọc tiếp
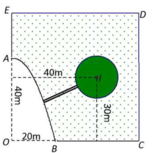
Một cái ao có hình ABCDE (như hình vẽ), ở giữa ao có một mảnh vườn hình tròn bán kính 10m, người ta muốn bắc một cây cầu từ bờ AB của ao đến vườn. Hỏi độ dài ngắn nhất l của cây cầu gần nhất với so nào dưới đây biết.
- Hai bờ AE và BC nằm trên hai đường thẳng vuông góc với nhau, hai đường thẳng này cắt nhau tại điểm O;
- Bờ AB là một phần của một parabol có đỉnh là điểm A và có trục đối xứng là đường thẳng OA ;
- Độ dài đoạn OA và OB lần lượt là 40m và 20m;
- Tâm I của mảnh vườn cách đường thẳng AE và BC lần lượt là 40m và 30m.
A. 29,7m
B. 17,7m
C. 11,7m
D. 6,7m





