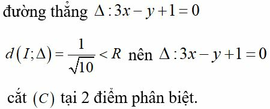
Chọn A.
Gọi I(0;2) và M z ⇒ M I = 5 suy ra tập điểm biểu diễn của số phức z trong mặt phẳng tọa độ giao điểm của đường tròn (C) tâm I(0;2) bán kính R = 5 và
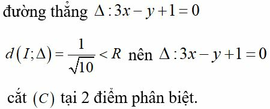
Cho số phức z=x+yi (x,y∈ R) thỏa mãn z+1-2i- z (1-i)=0. Trong mặt phẳng tọa độ Oxy, M là điểm biểu diễn của số phức z, M thuộc đường thẳng nào sau đây?
A. x+y-2=0.
B. x-y+2=0.
C. x+y-1=0.
D. x+y+1=0.
Cho số phức z=x+yi (x,y∈ R) thỏa mãn z+1-2i- z (1-i)=0. Trong mặt phẳng tọa độ Oxy, M là điểm biểu diễn của số phức z, M thuộc đường thẳng nào sau đây?
A. x+y-2=0.
B. x-y+2=0.
C. x+y-1=0.
D. x+y+1=0.
Cho các số phức z thỏa mãn z - i = z - 1 + 2 i . Tập hợp các điểm biểu diễn số phức w = ( 2 - i ) z + 1 trên mặt phẳng tọa độ là một đường thẳng. Phương trình đường thẳng đó là
A. x - 7 y - 9 = 0
B. x + 7 y - 9 = 0
C. x + 7 y + 9 = 0
D. x - 7 y + 9 = 0
Cho số phức z thay đổi hoàn toàn thỏa mãn: z − i = z − 1 + 2 i . Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức w thỏa mãn: w = 2 − i z + 1 là một đường thẳng. Viết phương trình đường thẳng đó.
A. − x + 7 y + 9 = 0.
B. x + 7 y − 9 = 0.
C. x + 7 y + 9 = 0.
D. x − 7 y + 9 = 0.
Cho các số phức z thỏa mãn |z+1-i|=|z-1+2i|. Tập hợp các điểm biểu diễn các số phức z trên mặt phẳng tọa độ là một đường thẳng. Viết phương trình đường thẳng đó
A. 4x+6y-3= 0
B. 4x-6y-3=0
C. 4x+6y+3=0
D. 4x-6y+3=0
Cho số phức z thỏa mãn: z − 1 + i = 2 . Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức z là:
A. Một đường thẳng
B. Một đường Parabol
C. Một đường tròn có bán kính bằng 2
D. Một đường tròn có bán kính bằng 4
Cho số phức z thỏa mãn z + 3 - 4 i = 5 . Biết rằng tập hợp điểm trong mặt phẳng tọa độ biểu diễn các số phức z là một đường tròn. Tim tọa độ tâm I và bán kính R của đường tròn đó.
A. I 3 ; - 4 , R = 5
B. I - 3 ; 4 , R = 5
C. I 3 ; - 4 , R = 5
D. I - 3 ; 4 , R = 5
Cho số phức z thỏa mãn z + 3 − 4 i = 5. Biết rằng tập hợp điểm trong mặt phẳng tọa độ biểu diễn các số phức z là một đường tròn. Tìm tọa độ tâm I và bán kính R của đường tròn đó.
A. I 3 ; − 4 , R = 5 .
B. I − 3 ; 4 , R = 5 .
C. I 3 ; − 4 , R = 5.
D. I − 3 ; 4 , R = 5.
Trong mặt phẳng tọa độ Oxy, cho số phức z thỏa mãn z - 1 + 2 i = 3 . Tập hợp các điểm biểu diễn cho số phức w=z(1+i) là đường tròn
A. Tâm I(3;-1); R = 3 2
B. Tâm I(3;-1);R=3
C. Tâm I(-3;1); R = 3 2
D. Tâm I(3;-1);R=3
