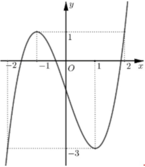
Đặt ![]() phương trình trở thành:
phương trình trở thành: ![]()
Đặt tiếp ![]() phương trình trở thành:
phương trình trở thành:
![]()
![]()
![]()

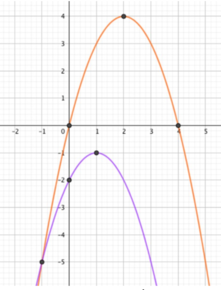
Với mỗi t > 0 cho duy nhất một nghiệm
x
=
log
3
t
phương trình có đúng hai nghiệm thực phân biệt khi và chỉ khi (*) có đúng hai nghiệm phân biệt
t
>
0
⇔
đường thẳng y cắt đồng thời hai parabol ![]() tại đúng hai điểm có hoành độ dương
tại đúng hai điểm có hoành độ dương 
![]()
Vậy có tất cả 23 số nguyên thoả mãn yêu cầu bài toán.
Chọn đáp án B.