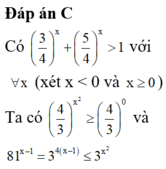Các câu hỏi tương tự
Cho hàm số f(x) liên tục trên
ℝ
và f(x)
≠
0 với mọi
x
∈
ℝ
.
f
(
x
)
(
2
x
+
1
)
f
2
(
x
)
và f(1)-0,5. Biết rằng tổng f(1)+f(2)+f(3)+...+f(2017)
a
b
với
a
b
tối giản. Mệnh đề...
Đọc tiếp
Cho hàm số f(x) liên tục trên ℝ và f(x) ≠ 0 với mọi x ∈ ℝ . f ' ( x ) = ( 2 x + 1 ) f 2 ( x ) và f(1)=-0,5. Biết rằng tổng f(1)+f(2)+f(3)+...+f(2017)= a b với a b tối giản.
Mệnh đề nào dưới đây đúng?
![]()
![]()
![]()
![]()
Có bao nhiêu mệnh đề sau là đúng?
1
6
x
≥
1
∀
x
∈
ℝ
2
x
2
2
x
-
1
∀
x
∈
ℝ
3
x
+
1...
Đọc tiếp
Có bao nhiêu mệnh đề sau là đúng?
1 6 x ≥ 1 ∀ x ∈ ℝ
2 x 2 > 2 x - 1 ∀ x ∈ ℝ
3 x + 1 > 2 x ∀ x ∈ ℝ
log 3 x 2 ≥ 0 ∀ x ≠ 0
a - b 2 a - 2 b ≥ 0 ∀ a , b ∈ ℝ
A. 2
B. 3
C. 4
D. 5
Cho a, b, c là các số thực dương,
a
≠
1
. Xét các mệnh đề sau: (I)
2
a
3
⇔
a
log
2
3
(II)
∀
x
∈
ℝ
0
,
log...
Đọc tiếp
Cho a, b, c là các số thực dương, a ≠ 1 . Xét các mệnh đề sau:
(I) 2 a = 3 ⇔ a = log 2 3
(II) ∀ x ∈ ℝ \ 0 , log 3 x 2 = 2 log 3 x
(III) log a b . c = log a b . log a c
Trong ba mệnh đề (I), (II), (III), tổng số mệnh đề đúng là?
A. 3
B. 2
C. 1
D. 0
Cho hàm số f(x) có đạo hàm f ' ( x ) = x 2 ( x - 1 ) 3 ( x - 2 ) 4 ( x - 3 ) 5 , ∀ x ∈ ℝ . Số điểm cực trị của hàm số đã cho là
A. 1
B. 4
C. 2
D. 3
Cho hàm số f(x)0 với
x
∈
ℝ
,
f
(
0
)
1
và
f
(
x
)
x
+
1
.
f
(
x
)
với mọi
x
∈
ℝ
. Mệnh đề nào dưới đây đúng?
Đọc tiếp
Cho hàm số f(x)>0 với x ∈ ℝ , f ( 0 ) = 1 và f ( x ) = x + 1 . f ' ( x ) với mọi x ∈ ℝ . Mệnh đề nào dưới đây đúng?
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
d
1
:
x
-
1
1
y
+
3
-
2
z
+
3
-
3
và ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d 1 : x - 1 1 = y + 3 - 2 = z + 3 - 3 và
d 2 : x = 3 t y = - 1 + 2 t , ( t ∈ ℝ ) z = - 1 3 t .
Mệnh đề nào dưới đây đúng?
![]()
![]()
![]()
![]()
Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = ( x 2 - 1 ) ( x + 2 ) 3 , ∀ x ∈ ℝ . Hàm số có bao nhiêu điểm cực trị?
A. 3
B. 2
C. 5
D. 1
Cho hàm số
f
x
1
3
+
2
x
+
1
3
+
2
-
x
. Trong các khẳng định sau có bao nhiêu khẳng định sai? 1.
f
x
≠
0...
Đọc tiếp
Cho hàm số f x = 1 3 + 2 x + 1 3 + 2 - x . Trong các khẳng định sau có bao nhiêu khẳng định sai?
1. f ' x ≠ 0 với mọi x ∈ ℝ
2. f 1 + f 2 + . . . + f 2017 = 2017
3. f x 2 = 1 3 + 4 x 1 3 + 4 - x
A. 1
B. 2
C. 3
D. 4
Cho hàm số f ( x ) có đạo hàm f ' ( x ) = ( x + 1 ) 2 ( x - 2 ) 3 ( 2 x + 3 ) , ∀ x ∈ ℝ . Số điểm cực trị của hàm số đã cho là
A. 2
B. 6
C. 1
D. 3
Cho hàm số f ( x ) có đạo hàm f ' ( x ) = ( x - 1 ) 2 ( x - 3 ) 3 ( 2 x + 3 ) , ∀ x ∈ ℝ . Số cực trị của hàm số đã cho là
A. 1
B. 2
C. 0
D. 3