Đáp án B.
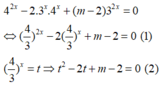
(1) có nghiệm dương ⇔ (2) có nghiệm lớn hơn 1
Đáp án B.
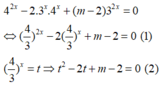
(1) có nghiệm dương ⇔ (2) có nghiệm lớn hơn 1
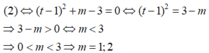
Cho hàm số y=f(x) liên tục trên tập ℝ và có đồ thị (C) như hình vẽ. Có bao nhiêu giá trị nguyên dương của tham số m để phương trình f 2 x - m - 1 f x + m - 2 = 0 có 12 nghiệm phân biệt?
A. Không tồn tại m
B. 1
C. 2
D. 3
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình 16 x - 2 . 12 x + ( m - 2 ) 9 x = 0 có nghiệm dương?
A. 1.
B. 2.
C. 4.
D. 3
Có bao nhiêu giá trị nguyên dương của tham số m để tập nghiệm của bất phương trình ( 3 x + 2 - 3 ) ( 3 x - 2 m ) < 0 chứa không quá 9 số nguyên?
A. 3281.
B. 3283.
C. 3280.
D. 3279.
Cho hàm số f x = 1 + x + x 2 2 ! + x 3 3 ! + . . . + x 2019 2019 ! - x 2 - 10 x k h i x < 0 . Hỏi có bao nhiêu giá trị nguyên dương và chia hết cho 5 của tham số m để bất phương trình m - f x ≤ 0 có nghiệm?
A. 5
B. 25
C. 6
D. 0
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình 16 x - 2 . 12 x + m - 2 . 9 x = 0 có nghiệm dương?
A. 2.
B. 3.
C. 4.
D. 1.
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình 16 x − 2.12 x + m − 2 9 x = 0 có nghiệm dương?
A. 1
B. 2
C. 4
D. 3
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình 16 x − 2.12 x + m − 2 .9 x = 0 có nghiệm dương?
A. 1
B. 2
C. 4
D. 3
Có bao nhiêu giá trị nguyên dương của tham số m để bất phương trình sau có nghiệm với mọi
x
∈
1
;
2
: ![]()
A. 3
B. 2
C. 1
D. 4
Có bao nhiêu giá trị nguyên của tham số m để phương trình 6 + x - 2 - x - 3 + x - 6 - x - 5 - m = 0 có nghiệm thực
A. 0
B. 2
C. 3
D. 1