Question

Có bao nhiêu giá trị nguyên của tham số m để: \(\overset{max\left|x^3-3x+m\right|}{\left[0;2\right]}+\overset{min\left|x^3-3x+m\right|}{\left[0;2\right]}=3\)

Answer 1

Đặt \(f\left(x\right)=x^3-3x+m\)

\(f'\left(x\right)=3x^2-3\)

\(f'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)

bbt:

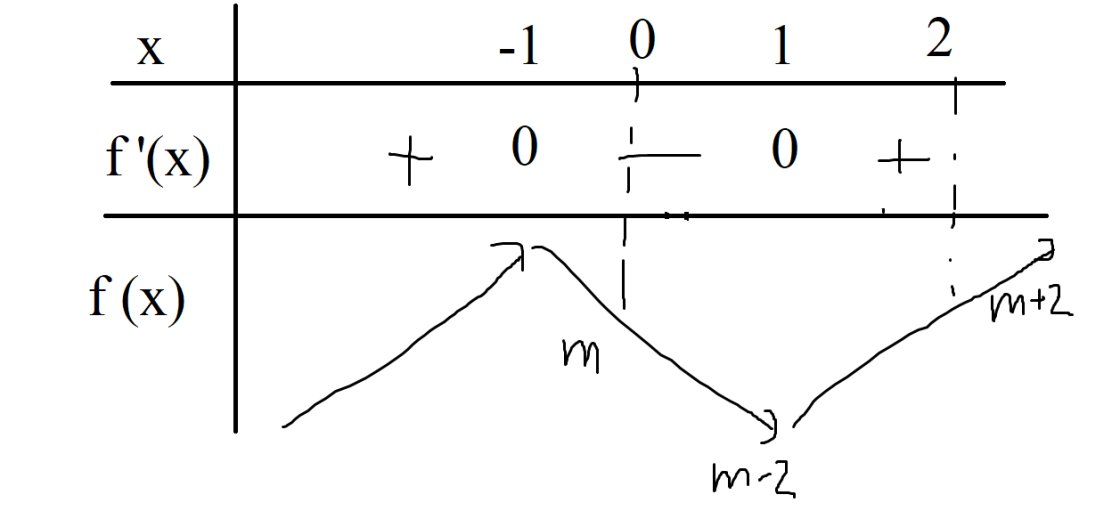
bbt của \(y=\left|f\left(x\right)\right|\) là bbt của \(f\left(x\right)\) giữ nguyên phần nằm trên trục hoành và lấy đối xứng phần nằm dưới trục hoành qua trục hoành

Xét \(m-2\ge0\Rightarrow m\ge2\)

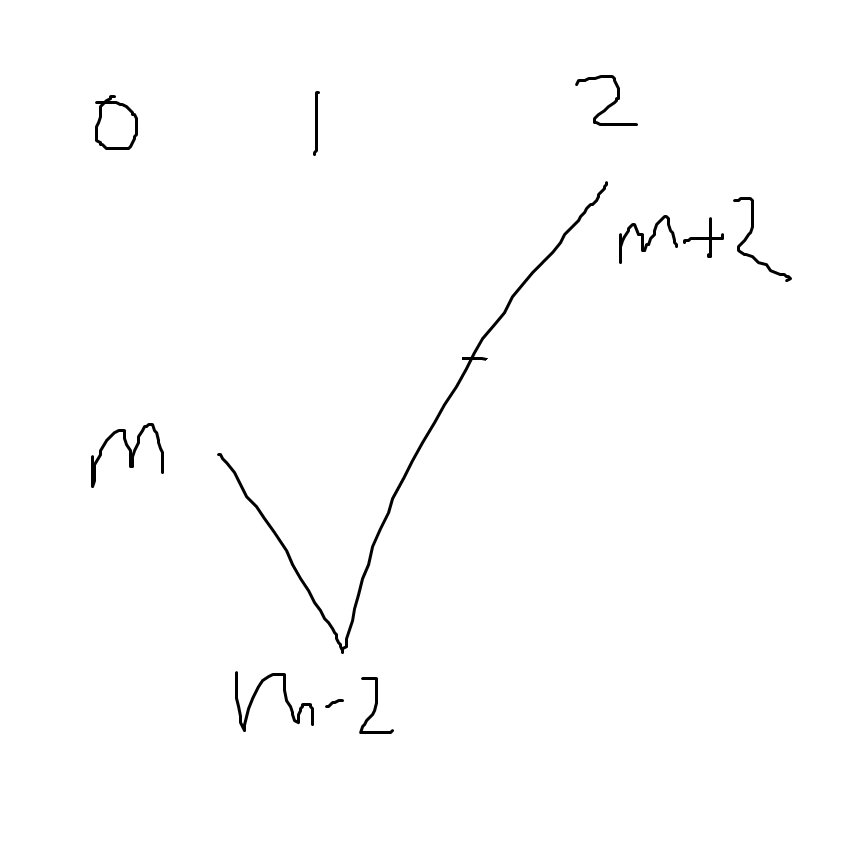
Theo bbt \(\Rightarrow y_{min\left[0,2\right]}+y_{max\left[0,2\right]}=y\left(1\right)+y\left(2\right)=m-2+m+2=2m\)

\(\Rightarrow2m=3\Rightarrow m=\dfrac{3}{2}\) (loại)

Xét \(m+2\le0\Rightarrow m\le-2\)

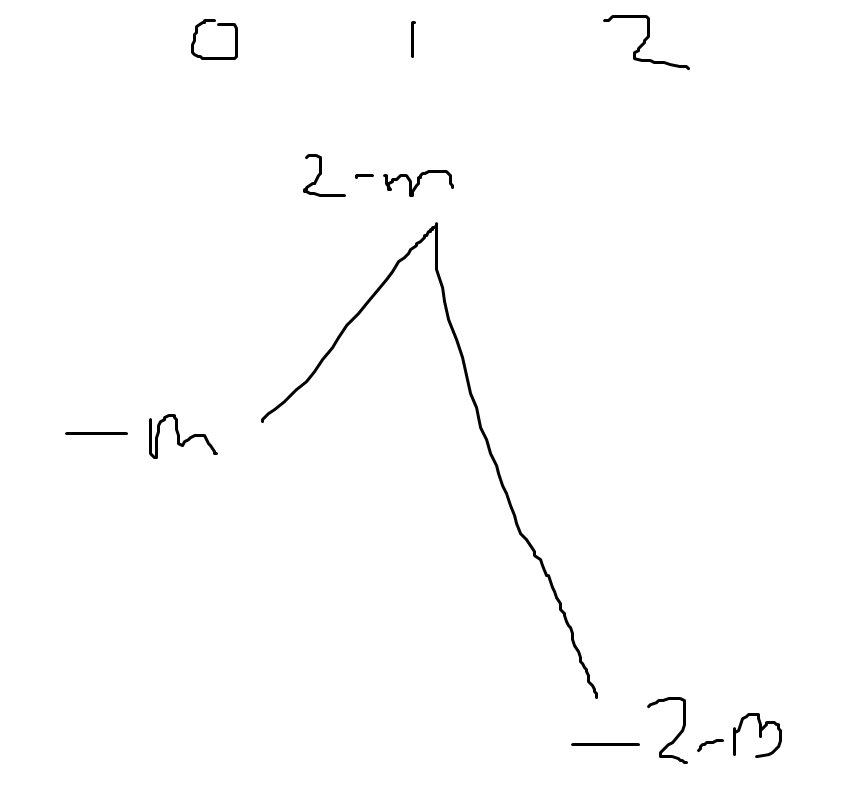
\(\Rightarrow y_{max\left[0,2\right]}+y_{min\left[0,2\right]}=y\left(2\right)+y\left(1\right)=-2-m+2-m=-2m\)

\(\Rightarrow-2m=3\Rightarrow m=-\dfrac{3}{2}\) (loại)

Xét \(-2< m< 2\) thì \(y_{min\left[0,2\right]}=0\) còn \(y_{max\left[0,2\right]}=y\left(1\right)\) hoặc \(y\left(2\right)\)

\(TH_1:y\left(1\right)\) là max thì \(2-m+0=3\Rightarrow m=-1\Rightarrow y\left(2\right)=m+2=1< y\left(1\right)\) (thỏa)

\(TH_2:y\left(2\right)\) là max thì \(m+2+0=3\Rightarrow m=1\Rightarrow f\left(1\right)=2-m=1< f\left(2\right)\) (thỏa)

Trong trường hợp này thì bbt của \(y=\left|f\left(x\right)\right|\) sẽ theo 2 dạng như này:

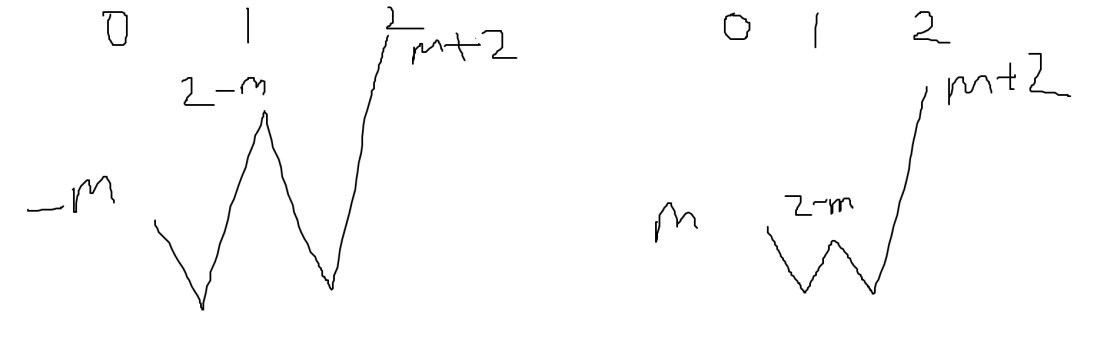
Vậy có 2 giá trị nguyên \(m\in\left\{-1,1\right\}\) thỏa đề