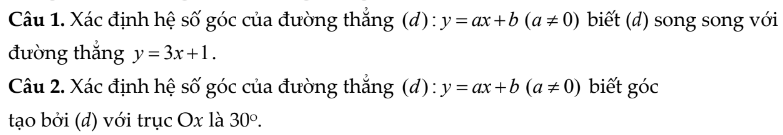a.
ĐKXĐ: \(\left[{}\begin{matrix}x\ge-1+\sqrt{2}\\x\le-1-\sqrt{2}\end{matrix}\right.\)
\(x^2-2x-1+2\left(x-1\right)\sqrt{x^2+2x-1}=0\)
\(\Leftrightarrow\left(x^2+2x-1\right)+2\left(x-1\right)\sqrt{x^2+2x-1}-4x=0\)
\(\Delta'=\left(x-1\right)^2+4x=\left(x+1\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x^2+2x-1}=1-x+x+1\\\sqrt{x^2+2x-1}=1-x-x-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x^2+2x-1}=2\\\sqrt{x^2+2x-1}=-2x\left(x\le0\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x^2+2x-1=4\\x^2+2x-1=4x^2\left(vô-nghiệm\right)\end{matrix}\right.\)
\(\Rightarrow x\)
b.
ĐKXĐ: \(x\ge-\sqrt[3]{3}\)
\(x^3+3-\left(5x-1\right)\sqrt{x^3+3}+6x^2-2x=0\)
Đặt \(\sqrt{x^3+3}=t\ge0\)
\(\Rightarrow t^2-\left(5x-1\right)t+6x^2-2x=0\)
\(\Delta=\left(5x-1\right)^2-4\left(6x^2-2x\right)=\left(x-1\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}t=\dfrac{5x-1-x+1}{2}=2x\\t=\dfrac{5x-1+x-1}{2}=3x-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x^3+3}=2x\left(x\ge0\right)\\\sqrt{x^3+3}=3x-1\left(x\ge\dfrac{1}{3}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^3+2=4x^2\left(x\ge0\right)\\x^3+3=9x^2-6x+1\left(x\ge\dfrac{1}{3}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(x-1\right)\left(x^2-3x-3\right)=0\left(x\ge0\right)\\\left(x-1\right)\left(x^2-8x-2\right)=0\left(x\ge\dfrac{1}{3}\right)\end{matrix}\right.\)
\(\Leftrightarrow...\)

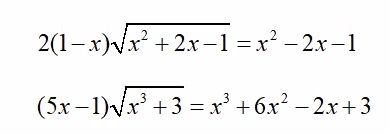










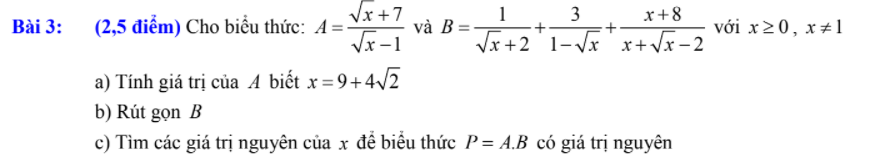 được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều.
được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều. 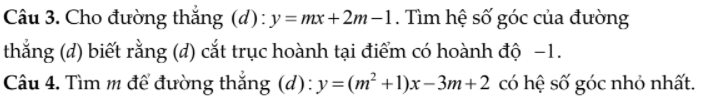 này được
này được