a) Khi \(m=2\),ta có phương trình :
\(\left(\sqrt{x}-1\right)\left(x^2-2\left(2+1\right)x+2^2+2.2\right)=0\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)\left(x^2-6x+8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}-1=0\\x^2-6x+8=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\left(x\ge0\right)\\x=2\cup x=4\end{matrix}\right.\)
Vậy phương trình cho có 3 nghiệm \(\left[{}\begin{matrix}x=1\\x=2\\x=4\end{matrix}\right.\)
b) \(\left(\sqrt{x}-1\right)\left(x^2-2\left(m+1\right)x+m^2+2m\right)=0\left(1\right)\)
Để (1) có 3 nghiệm phân biệt khi và chỉ khi phương trình
\(x^2-2\left(m+1\right)x+m^2+2m=0\) có 2 nghiệm phân biệt đều khác 1
\(\Leftrightarrow\Delta'=\left(m+1\right)^2-\left(m^2+2m\right)>0\)
\(\Leftrightarrow m^2+2m+1-m^2-2m>0\)
\(\Leftrightarrow\Delta'=1>0,\forall m\in R\left(1\right)\)
\(\Rightarrow\left[{}\begin{matrix}x=m+2\\x=m\end{matrix}\right.\)
2 nghiệm phân biệt khác 1
\(\Rightarrow\left\{{}\begin{matrix}m+2\ne1\\m\ne1\end{matrix}\right.\) \(\Leftrightarrow m\ne\pm1\left(2\right)\)
\(x_1^3+x_2^3+x_3^3=9\)
\(\Leftrightarrow1^3+\left(x_2+x_3\right)\left(x_2^2+x_3^2-x_2x_3\right)=9\)
\(\Leftrightarrow\left(x_2+x_3\right)\left[\left(x_2+x_3\right)^2-3x_2.x_3\right]-8=0\)
\(\Leftrightarrow2\left(m+1\right)\left[4\left(m+1\right)^2-3\left(m^2+2m\right)\right]-8=0\)
\(\Leftrightarrow2\left(m+1\right)\left(4m^2+4m+4-3m^2-6m\right)-8=0\)
\(\Leftrightarrow\left(m+1\right)\left(m^2-2m+4\right)-4=0\)
\(\Leftrightarrow m^3-2m^2+4m+m^2-2m+4-4=0\)
\(\Leftrightarrow m^3-m^2+2m=0\)
\(\Leftrightarrow m\left(m^2-m+2\right)=0\)
mà \(m^2-m+2>0,\forall m\in R\left(\Delta=-7< 0;1>0\right)\)
\(\Rightarrow m=0\left(3\right)\)
\(\left(1\right);\left(2\right);\left(3\right)\Rightarrow m=0\) thỏa mãn yêu cầu đề bài.

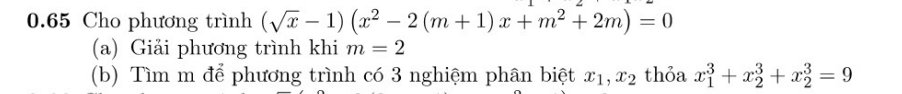





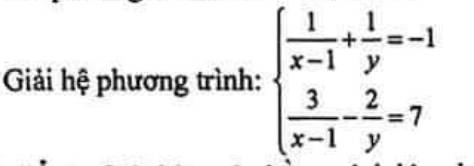 cíu lẹ ạ!
cíu lẹ ạ!





 Giải giúp tớ với ạ, tớ cần gấp lắm
Giải giúp tớ với ạ, tớ cần gấp lắm



