Question

Chứng minh:

\(\left(\sqrt{2006}-\sqrt{2005}\right)\)và \(\left(\sqrt{2006}+\sqrt{2005}\right)\)là 2 số nghịch đảo của nhau.

Answer 1

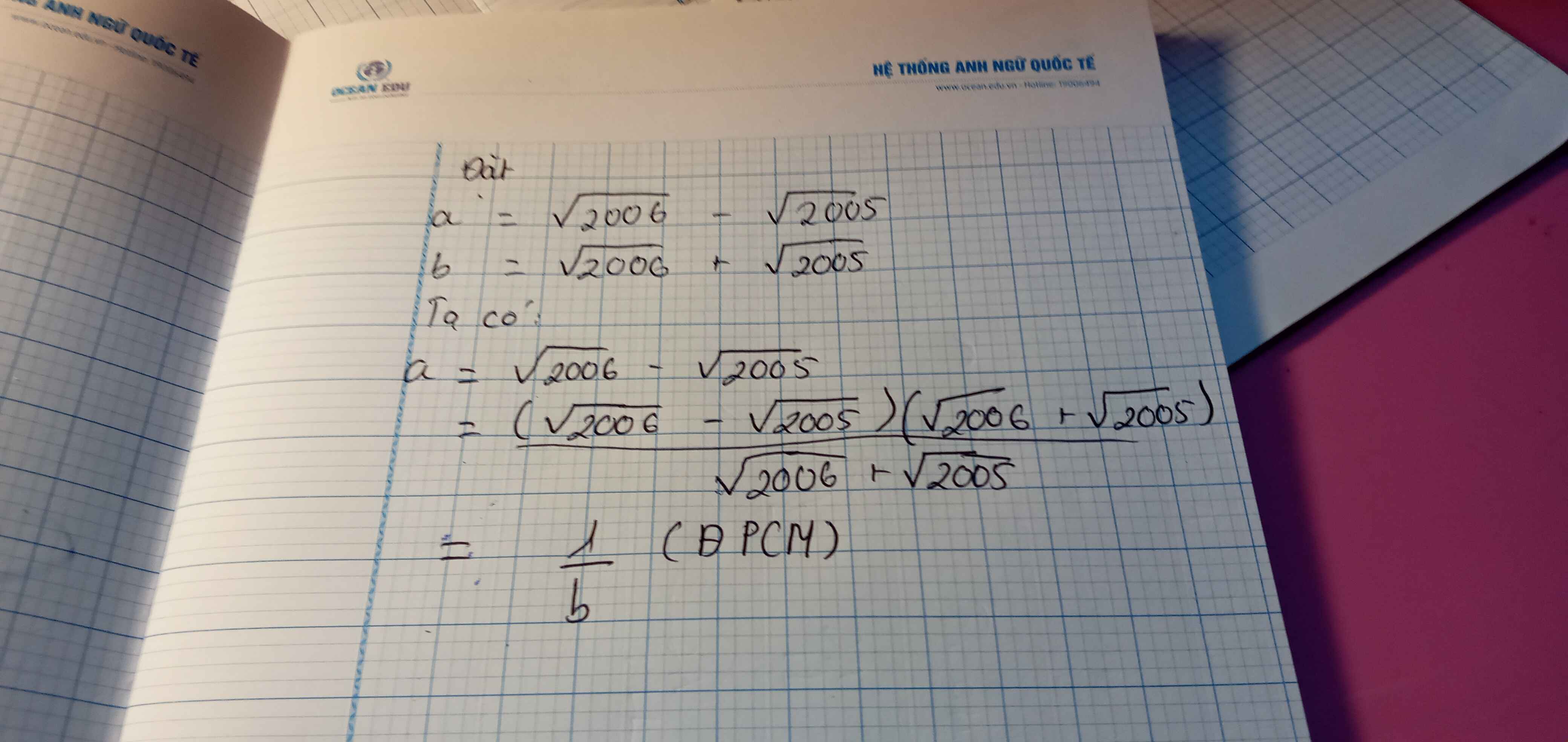
Đặt \(a=\sqrt{2006}-\sqrt{2005};b=\sqrt{2006}+\sqrt{2005}\)

Ta có 

\(a=\sqrt{2006}-\sqrt{2005}=\dfrac{\left(\sqrt{2006}-\sqrt{2005}\right)\left(\sqrt{2006}+\sqrt{2005}\right)}{\sqrt{2006}+\sqrt{2005}}=\dfrac{1}{b}\)

\(\RightarrowĐfcm\)

Answer 2

Answer 3

\(\sqrt{2006}-\sqrt{2005}=\dfrac{1}{\sqrt{2006}+\sqrt{2005}}\)

Do đó: \(\sqrt{2006}-\sqrt{2005};\sqrt{2006}+\sqrt{2005}\) là hai số nghịch đảo