Question

Chứng minh rằng trong một tứ giác tổng độ dài hai đường chéo bao giờ cũng lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tứ giác đó.

Answer 1

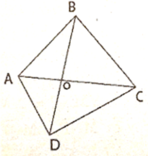
Đặt p = AB + BC + CD + DA

Ta có: OA + OD > AD (1)

OA + OB > AB (2)

OB + OC > BC (3)

OC + OD > CD (4)

Cộng vế theo vế (1), (2), (3), (4) ta có:

2(OA + OB + OC + OD) > AB + BC + CD + DA

2(AC + BD) > p

AC + BD > p/2 (*)

Mặt khác: Trong ΔABC có AC < AB + BC (5)

Trong ΔACD có AC < AD + CD (6)

Cộng vế theo vế (5) và (6) ta có:

2AC < AB + BC + CD + DA

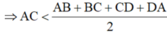
Tương tự ta cũng có BD < p/2. Suy ra: AC + BC < (p/2) + (p/2)

Hay AC + BD < p (**)

Từ (*) và (**) ta có: (p/2) < AC + BD < p.