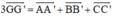Các câu hỏi tương tự
Các điểm A'(-4; 1), B'(2; 4), C'(2; -2) lần lượt là trung điểm các cạnh BC, CA và AB của tam giác ABC. Tính tọa độ các đỉnh của tam giác ABC. Chứng minh rằng trọng tâm của tam giác ABC và A'B'C' trùng nhau.
Cho tam giác ABC và điểm M nằm trong tam giác. Gọi AM, BM, CM cắt BC, CA, AB lần lượt tại A', B', C'. Chứng minh rằng M là trọng tâm tam giác ABC khi và chỉ khi M là trọng tâm tam giác A'B'C'
Cho hai tam giác ABC và ABC lần lượt có trọng tâm là G và G. Đẳng thức nào sau đây là sai? A. B. C. D.
Đọc tiếp
Cho hai tam giác ABC và A'B'C' lần lượt có trọng tâm là G và G'. Đẳng thức nào sau đây là sai?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho G và G' lần lượt là trọng tâm của tam giác ABC và A'B'C' Tính tổng vecto AA'+BB'+CC'
Cho tam giác ABC, A(4;0) B(2;-4) C(0;-2). Gọi G là trọng tâm tam giác ABC. GỌi M, N, P lần lượt là trung điểm các cạnh BC, CA, AB. Chứng minh tam giác ABC, tam giác MNP có cùng trọng tâm
Các tam giác ABC và A’B’C’ có trọng tâm lần lượt là G và G’. Khẳng định nào sau đây là đúng? A.
A
A
→
+
B
B
→
+
C
C
→
G...
Đọc tiếp
Các tam giác ABC và A’B’C’ có trọng tâm lần lượt là G và G’. Khẳng định nào sau đây là đúng?
A. A A ' → + B B ' → + C C ' → = G G ' →
B. A A ' → + B B ' → + C C ' → = 1 3 G G ' →
C. A A ' → + B B ' → + C C ' → = 3 G G ' →
D. A A ' → + B B ' → + C C ' → = 0 →
Cho hai tam giác $A B C$ và $A_{1} B_{1} C_{1}$ có cùng trọng tâm $\mathrm{G}$. Gọi $G_{1}, G_{2}, G_{3}$ lần lượt là trọng tâm tam giác $B C A_{1}, A B C_{1}, A C B_{1}$. Chứng minh rằng $\overrightarrow{G G_{1}}+\overrightarrow{G G_{2}}+\overrightarrow{G G_{3}}=\overrightarrow{0}$
Tam giác ABC có trọng tâm G, độ dài các cạnh BC, CA, AB lần lượt là a, b, c. Khi đó ABC là tam giác đều nếu có điều kiện nào sau đây? A.
a
G
A
→
+
b
G
B
→
+
c
G
C
→
0...
Đọc tiếp
Tam giác ABC có trọng tâm G, độ dài các cạnh BC, CA, AB lần lượt là a, b, c. Khi đó ABC là tam giác đều nếu có điều kiện nào sau đây?
A. a G A → + b G B → + c G C → = 0 →
B. a G A → + b G B → - c G C → = 0 →
C. a G A → - b G B → + c G C → = 0 →
D. - a G A → + b G B → + c G C → = 0 →
cho 4 điểm a b c d g là trọng tâm của tam giác abc b là trọng tâm của DG chứng minh rằng DA-5DB+DC=0