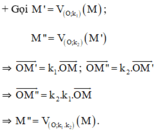
Vậy khi thực hiện liên tiếp hai phép vị tự tâm O với tỉ số k1 và k2 thì ta được 1 phép vị tự tâm O với tỉ số k1.k2.
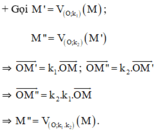
Vậy khi thực hiện liên tiếp hai phép vị tự tâm O với tỉ số k1 và k2 thì ta được 1 phép vị tự tâm O với tỉ số k1.k2.
Cho (C): x − 2 2 + y + 6 2 = 4 . Thực hiện liên tiếp phép vị tự tâm O tỉ số k = − 1 2 và phép quay tâm O góc 90 ° sẽ biến(C) thành đường tròn nào?
A. x + 3 2 + y + 1 2 = 4
B. x − 3 2 + y + 1 2 = 4
C. x + 3 2 + y − 1 2 = 1
D. x + 3 2 + y + 1 2 = 1
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x - 1 2 + y - 2 2 = 4 . Phép đồng dạng thực hiện bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k= - 2 và phép quay tâm O góc quay 180 ∘ , khi đó đường tròn (C) sẽ biến thành đường tròn nào sau đây
A. x 2 + y 2 - 4 x - 8 y - 2 = 0
B. x 2 + y 2 + 4 x + 8 y + 2 = 0
C. x + 2 2 + y + 4 2 = 16
D. x - 2 2 + y - 4 2 = 16
Cho M(4;4). Thực hiện liên tiếp phép vị tự tâm O tỉ số k = 3 và phép tịnh tiến theo u → − 2 ; − 3 sẽ biến M thành điểm nào?
A. 10 ; 9
B. 9 ; 10
C. − 10 ; − 9
D. − 9 ; − 10
Trong mặt phẳng Oxy cho điểm M(2;4). Hỏi phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k = 1/2 và phép đối xứng trục Oy sẽ biến điểm M thành điểm nào sau đây?
A. (-2;4)
B. (-1;2)
C. (1;2)
D. (1;-2)
Trong mặt phẳng Oxy cho điểm I(1;1) và đường tròn tâm I bán kính 2. Viết phương trình đường tròn là ảnh của đường tròn trên qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O, góc 45 o và phép vị tự tâm O, tỉ số căn 2 .
Số phát biểuđúng:
1. Qua phép vị tự có tỉ số k ≠ 0 , đường thẳng đi qua tâm vị tự sẽ biến thành chính nó
2. Qua phép vị tự có tỉ số k ≠ 0 , đường tròn có tâm là tâm vị tự sẽ biến thành chính nó.
3. Qua phép vị tự có tỉ số k ≠ 1 , không có đường tròn nào biến thành chính nó.
4. Qua phép vị tự V(O;1), đường tròn tâm O sẽ biến thành chính nó.
5. Phép vị tự tỉ số k biến đường thẳng thành đường thẳng song song hoặc trùng với đường thẳng đó
6. Phép vị tự tỉ số k biến đoạn thẳng thành đoạn thẳng mà độ dài được nhân lên với hệ số k
7. Trong phép vị tự tâm O, tỉ số k, nếu k < 0 thì điểm M và ảnh của nó ở về hai phía đối với tâm O.
8. Mọi phép dời hình đều là phép đồng dạng với tỉ số k = 1
9. Phép hợp thành của một phép vị tự tỉ số k và một phép đối xứng tâm là phép đồng dạng tỉ số
10. Hai đường tròn bất kì luôn có phép vị tự biến đường này thành đường kia
11. Khi k = 1 , phép vị tự là phép đồng nhất
12. Phép vị tự biến tứ giác thành tứ giác bằng nó
13. Khi k = 1, phép đồng dạng là phép dời hình
14. Phép đối xứng tâm là phép đồng dạng tỉ số k = 1
A.9
B.10
C.11
D.12
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(0;−1) , bán kính R = 2. Ảnh của (C) qua việc thực hiện liên tiếp phép quay tâm O góc quay 180 ° và phép vị tự tâm O tỉ số 2
A. ( x − 2 ) 2 + y 2 = 16
B. x 2 + y − 2 2 = 4
C. ( x − 2 ) 2 + y 2 = 4
D. x 2 + y − 2 2 = 16
Trong mặt phẳng Oxy cho đường thẳng d có phương trình x = 2 2 . Hãy viết phương trình đường thẳng d’ là ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k = 0,5 và phép quay tâm O góc 45 ο
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(0;−1) , bán kính R = 3. Ảnh của (C) qua việc thực hiện liên tiếp phép quay tâm O góc quay 180 ° và phép vị tự tâm O tỉ số 2, phép tịnh tiến theo vectơ u → 1 ; 2
A. x − 4 2 + y − 1 2 = 9
B. x − 1 2 + y − 4 2 = 9
C. x − 1 2 + y − 4 2 = 36
D. x − 4 2 + y − 1 2 = 36