Xét hình thoi ABCD, kẻ hai đường cao
AH ⊥ BC, AK ⊥ CD.
Ta cần chứng minh: AH = AK.
Áp dụng định nghĩa, tính chất về góc và giả thiết của hình thoi ABCD, ta có:
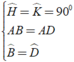 ⇒ Δ ABH = Δ ADH ( g - c - g )
⇒ Δ ABH = Δ ADH ( g - c - g )
⇒ AH = AK (cặp cạnh tương ứng bằng nhau)
→ (đpcm)
Xét hình thoi ABCD, kẻ hai đường cao
AH ⊥ BC, AK ⊥ CD.
Ta cần chứng minh: AH = AK.
Áp dụng định nghĩa, tính chất về góc và giả thiết của hình thoi ABCD, ta có:
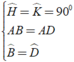 ⇒ Δ ABH = Δ ADH ( g - c - g )
⇒ Δ ABH = Δ ADH ( g - c - g )
⇒ AH = AK (cặp cạnh tương ứng bằng nhau)
→ (đpcm)
Chứng minh rằng các đường cao của hình thoi bằng nhau
a) cho hình thoi ABCD . kẻ hai đường cao AH , AK . Chứng minh rằng AH=AK
b) hình bình hành ABCD có hai đường cao AH,AK bằng nhau . Chứng minh rằng ABCD là hình thoi
Hình bình hành ABCD có hai đường cao AH, AK bằng nhau. Chứng minh rằng ABCD là hình thoi
Chứng minh răng các đường cao của hinh thoi bằng nhau
Chứng Minh:
1, Các góc đối nhau bằng nhau là hình thoi
2,Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường là hình thoi
3, Hai đường chéo là các đường phân giác của các góc của hình thoi.
4,Hình thoi có tất cả tính chất của hình bình hành.
Bài 1:Chứng minh rằng trung điểm 4 cạnh của 1 hình chữ nhật là đỉnh của hình thoi
Bài 2:Chứng minh rằng trung điểm các cạnh của 1 hình thoi là đỉnh cao của 1 hình chữ nhật
bạn nào bít chỉ với , cần gấp:
chứng minh rằng các trung điểm của bốn cạnh hình chữ nhật là các đỉnh của hình thoi. là theo tính chất hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
cho tứ giác abcd có hai đường chéo cắt nhau tại o. Chứng minh rằng nếu các tam giác aob, boc, cod, doa có chu vi bằng nhau thì tứ giác abcd là hình thoi
Cho hình bình hành ABCD, các đường chéo cắt nhau tại O. Gọi E,F,G,H theo thứ tự là giao điểm của các đường phân giác của tam giác AOB, BOC, COD, DOA. Chứng minh rằng EFGH là hình thoi.