Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Các câu hỏi tương tự
Cho hình vẽ:Cho đường tròn (I;r) nội tiếp tam giác ABC tiếp xúc với BC, CA, AB lần lượt tại D, E, F. DN, EK, FL là các đường kính của (I). Qua N kẻ đường thẳng song song với BC cắt AC, AB lần lượt tại P và Q. a. Chứng minh: ∆BIQ vuông và QN BD r² b. Gọi M là trung điểm của BC. Chứng minh: AN // IM c. KL cắt BC tại S. Chứng minh; SI _|_ IM
Đọc tiếp
Cho hình vẽ:
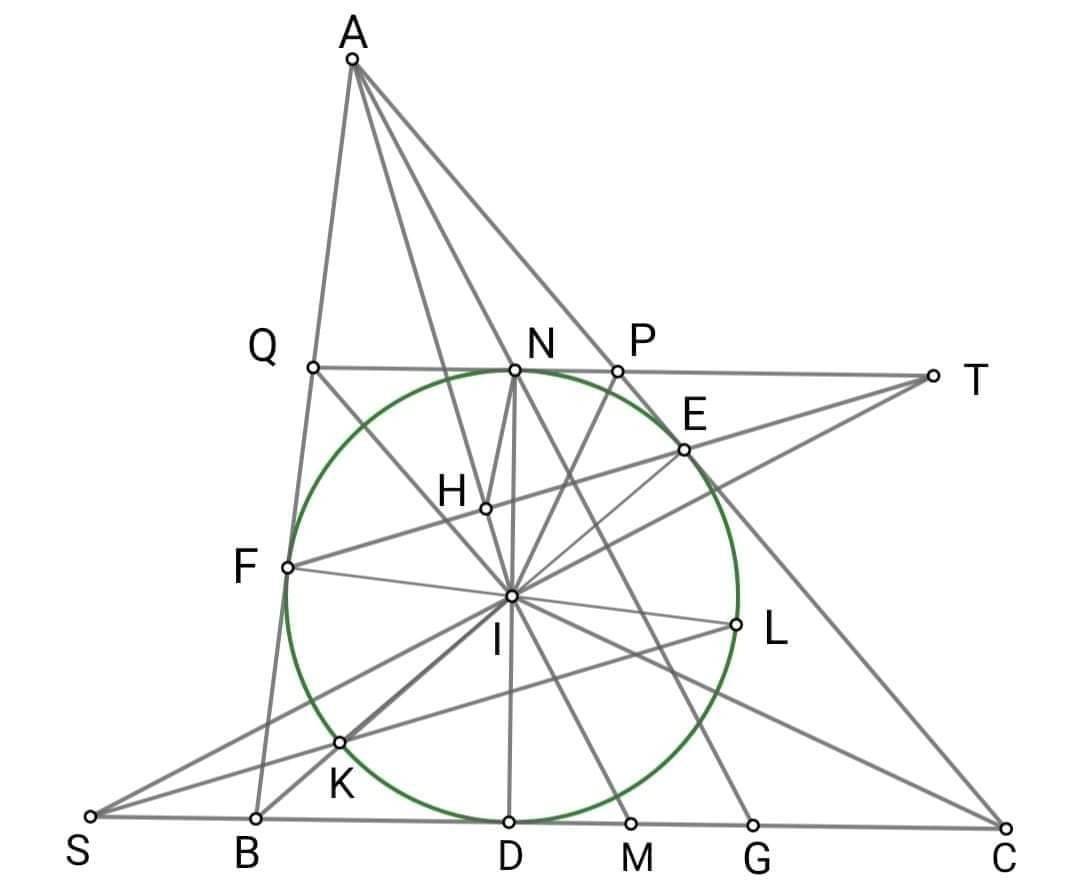Cho đường tròn (I;r) nội tiếp tam giác ABC tiếp xúc với BC, CA, AB lần lượt tại D, E, F. DN, EK, FL là các đường kính của (I). Qua N kẻ đường thẳng song song với BC cắt AC, AB lần lượt tại P và Q. a. Chứng minh: ∆BIQ vuông và QN BD = r² b. Gọi M là trung điểm của BC. Chứng minh: AN // IM c. KL cắt BC tại S. Chứng minh; SI _|_ IM
5 tháng 10 2016 lúc 22:00
Cho\(S\notin xy;I_1,I_2\in xy\).Trên nửa mặt phẳng bờ xy chứa S,vẽ 2 đường thẳng I1R1 và I2R2 cắt nhau tại S' sao cho\(\widehat{SI_1x}=\widehat{yI_1R_1};\widehat{xI_2S}=\widehat{yI_2R_2}\).Chứng minh xy là trung trực của SS'
Cho năm số thực m, n, p, q và r sao cho m/n=p/q=r/e Chứng minh (m+2n+3p+4q/n+2p+3q+4r)^4=m^4+n^4+p^4-q^4/n^4+p^4=q^4-r^4=m/r
cho các đa thức P=\(^{x^3-3x^4+4x-2}\), Q(x) =\(3x^4-x^2+2x-4\), R(x)=\(x^3-3x^2-16\)
a) tính f(x)= p(x)+Q(x)-R(x)
b) chứng minh rằng 1 là nghiệm của đa thức P(x) Q(x) nhưng không là nghiệm của R(x)
c)chứng minh rằng f(x) không có nghiệm
Cho năm số thực m, n, p, q và r sao cho m/n=p/q=r/e Chứng minh (m+2n+3p+4q/n+2p+3q+4r)^4=m^4+n^4+p^4-q^4/n^4+p^4=q^4-r^4=m/r
Hộ mình vs
Cho tam giác ABC vuông tại A, đường cao AH. I và K là giao điểm các đường phân giác trong tam giác AHB và AHC. Gọi Q là giao điểm của BI và AK. R là giao điểm của CK và AI. O là giao điểm của BI và CK. Đường thẳng IK giao AB, AC lần lượt tại M và N.a) Chứng minh Delta AMN vưông cânb) Chứng minh AHAM từ đó chứng minh S_{AMN}lefrac{1}{2}S_{ABC}c) Chứng minh OA^22.RQ^2OA^22RQ^2MỌI NGƯỜI GIÚP EM VỚI
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH. I và K là giao điểm các đường phân giác trong tam giác AHB và AHC. Gọi Q là giao điểm của BI và AK. R là giao điểm của CK và AI. O là giao điểm của BI và CK. Đường thẳng IK giao AB, AC lần lượt tại M và N.
a) Chứng minh \(\Delta AMN\) vưông cân
b) Chứng minh AH=AM từ đó chứng minh \(S_{AMN}\le\frac{1}{2}S_{ABC}\)
c) Chứng minh OA^2=2.RQ^2\(OA^2=2RQ^2\)
MỌI NGƯỜI GIÚP EM VỚI
Chứng minh \(a^7-a⋮7\forall a\in R\)
12 tháng 3 2019 lúc 16:14
KIỂM TRA 5 PHÚT Đề bài : Cho bigtriangleup ABC. Các đường cao AH, BK, CL cắt nhau tại I. Gọi D, E, F lần lượt là trung điểm của BC, CA, AB ; gọi P, Q, R lần lượt là trung điểm của IA, IB, IC. 1/ Chứng minh PD, QE, RF đồng quy.2/ Gọi J là điểm đồng quy. Chứng minh I là trung điểm của mỗi đường.
Đọc tiếp
KIỂM TRA 5 PHÚT
Đề bài : Cho \(\bigtriangleup ABC\). Các đường cao AH, BK, CL cắt nhau tại I. Gọi D, E, F lần lượt là trung điểm của BC, CA, AB ; gọi P, Q, R lần lượt là trung điểm của IA, IB, IC.
1/ Chứng minh PD, QE, RF đồng quy.
2/ Gọi J là điểm đồng quy. Chứng minh I là trung điểm của mỗi đường.
Cho p , q , r và s là các số nguyên tố lớn hơn 3
Chứng minh rằng : p2 - q2 + r2 - s2 ⋮ 24