Gọi d = ƯCLN ( 4n + 3 ; 5n + 4 ) ; d ∈ N*
Ta có: d = ƯC( 4n + 3 ; 5n + 4 )
⇒ ( 4n + 3 ) ⋮ d ; ( 5n + 4 ) ⋮ d ⇒ [4( 5n + 4 ) – 5 ( 4n + 3 )] ⋮ d
⇒[( 20n + 16 ) – ( 20n + 15 )] ⋮ d ⇒ 1 ⋮ d. Mà d ∈ N* → d = 1
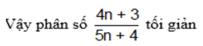
Gọi d = ƯCLN ( 4n + 3 ; 5n + 4 ) ; d ∈ N*
Ta có: d = ƯC( 4n + 3 ; 5n + 4 )
⇒ ( 4n + 3 ) ⋮ d ; ( 5n + 4 ) ⋮ d ⇒ [4( 5n + 4 ) – 5 ( 4n + 3 )] ⋮ d
⇒[( 20n + 16 ) – ( 20n + 15 )] ⋮ d ⇒ 1 ⋮ d. Mà d ∈ N* → d = 1
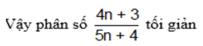
Chứng minh rằng phân số: 4n+3/5n+4 tối giản với mọi n thuộc N*
Chứng minh phân số: 4 n + 3 5 n + 4 tối giản với mọi n ∈ N *
Chứng minh rằng phân số sau tối giản với mọi số nguyên n : n^3 + 2n/n^4 + 3n^2 + 1
Chứng minh phân số: 4n+3/5n+4 tối giản với mọi n thuộc tập hợp N*
. Chứng minh rằng: Với mọi n thì phân số 7n+4/5n+3 là phân số tối giản
Chứng minh rằng : Với mọi n thì phân số \(\dfrac{7n+4}{5n+3}\) là phân số tối giản
a) Chứng minh rằng với mọi số tự nhiên n thì phân số 21n+4/14n+3 là phân số tối giản
b) Tìm tất cả các số tự nhiên n để phân số n+3/n-12 là phân số tối giản
c) Tìm các số tự nhiên n để phân số 21n+3/6n+4 rút gọn được
Chứng minh rằng : Với mọi n thì phân số 7n+4/5n+3 là phân số tối giản
\(\frac{n+1}{2n+3};\frac{8n+5}{6n+4};\frac{21n+4}{14n+3}\)Chứng minh rằng với mọi n thuộc N các phân số sau tối giản