Các câu hỏi tương tự
Cho khối chóp S.ABCD có đáy là hình thang với hai đáy là AB và CD, AB 2CD. Gọi E là một điểm trên cạnh SC. Mặt phẳng (ABE) chia khối chóp S.ABCD thành hai khối đa diện có thể tích bằng nhau. Tính tỉ số
S
E
S
C
Đọc tiếp
Cho khối chóp S.ABCD có đáy là hình thang với hai đáy là AB và CD, AB = 2CD. Gọi E là một điểm trên cạnh SC. Mặt phẳng (ABE) chia khối chóp S.ABCD thành hai khối đa diện có thể tích bằng nhau. Tính tỉ số S E S C
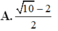
![]()
![]()
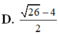
Cho hình chóp SABCD có đáy ABCD là hình chư nhật AB= 1 AD = √10 SA=SB, SC = SD và mặt phẳng (SAB)và (SCD) vuông góc với nhau đồng thời tổng diện tích của hai tam giác SAB và tam giác SCD bằng 2 Thể tích khối chóp SABCD bằng
Cho khối đa diện (kích thước như hình vẽ bên) được tạo bởi ba hình chữ nhật và hai tam giác bằng nhau. Tính thể tích khối đa diện đã cho A.
48
c
m
3
B.
192
c
m
3
C.
32
c
m
3
D.
96
c
m
3
Đọc tiếp
Cho khối đa diện (kích thước như hình vẽ bên) được tạo bởi ba hình chữ nhật và hai tam giác bằng nhau. Tính thể tích khối đa diện đã cho
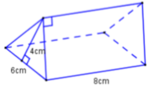
A. 48 c m 3
B. 192 c m 3
C. 32 c m 3
D. 96 c m 3
Cho khối lập phương ABCD.ABCD. Cắt khối lập phương bởi các mặt phẳng (ABD) và (CBD) ta được ba khối đa diện. Xét các mệnh đề sau: (I): Ba khối đa diện thu được gồm hai khối chóp tam giác đều và một khối lăng trụ tam giác. (II): Ba khối đa diện thu được gồm hai khối tứ diện và một khối bát diện đều. (III): Trong ba khối đa diện thu được có hai khối đa diện bằng nhau. Số mệnh đề đúng là A. 3. B. 2. C. 0. D. 1.
Đọc tiếp
Cho khối lập phương ABCD.A'B'C'D'. Cắt khối lập phương bởi các mặt phẳng (AB'D') và (C'BD) ta được ba khối đa diện. Xét các mệnh đề sau:
(I): Ba khối đa diện thu được gồm hai khối chóp tam giác đều và một khối lăng trụ tam giác.
(II): Ba khối đa diện thu được gồm hai khối tứ diện và một khối bát diện đều.
(III): Trong ba khối đa diện thu được có hai khối đa diện bằng nhau.
Số mệnh đề đúng là
A. 3.
B. 2.
C. 0.
D. 1.
Một khối đồ chơi gồm hai khối trụ (H1),(H2) xếp chồng lên nhau, lần lượt có bán kính đáy và chiều cao tương ứng là
r
1
,
h
1
,
r
2
,
h
2
thỏa mãn
r
2...
Đọc tiếp
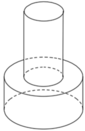
Một khối đồ chơi gồm hai khối trụ (H1),(H2) xếp chồng lên nhau, lần lượt có bán kính đáy và chiều cao tương ứng là r 1 , h 1 , r 2 , h 2 thỏa mãn r 2 = 1 2 r 1 , h 2 = 2 h 1 (tham khảo hình vẽ). Biết rằng thể tích của toàn bộ khối đồ chơi bằng 30 c m 3 thể tích của khối trụ (H1) bằng:
A. 24 c m 3
B. 15 c m 3
C. 20 c m 3
D. 10 c m 3
Một khối đồ chơi gồm hai khối trụ (H1),(H2) xếp chồng lên nhau, lần lượt có bán kính đáy và chiều cao tương ứng là r1 ,h1 ,r2 ,h2,
r
2
1
2
r
1
,
h
2
2
h...
Đọc tiếp
Một khối đồ chơi gồm hai khối trụ (H1),(H2) xếp chồng lên nhau, lần lượt có bán kính đáy và chiều cao tương ứng là r1 ,h1 ,r2 ,h2, r 2 = 1 2 r 1 , h 2 = 2 h 1 thỏa mãn (tham khảo hình vẽ).
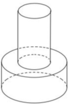
Biết rằng thể tích của toàn bộ khối đồ chơi bằng 30cm3, thể tích khối trụ (H1) bằng:
A. 24cm3
B. 15cm3
C. 20cm3
D. 10cm3
Một khối đồ chơi gồm hai khối trụ
H
1
,
H
2
xếp chồng lên nhau, lần lượt có bán kính đáy và chiều cao tương ứng là
r
1
,
h
1
,
r
2
,
h
2
th...
Đọc tiếp
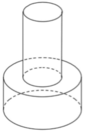
Một khối đồ chơi gồm hai khối trụ H 1 , H 2 xếp chồng lên nhau, lần lượt có bán kính đáy và chiều cao tương ứng là r 1 , h 1 , r 2 , h 2 thỏa mãn r 2 = 1 2 r 1 , h 2 = 2 h 1 (tham khảo hình vẽ bên). Biết rằng thể tích của toàn bộ khối đồ chơi bằng 30 c m 3 , thể tích khối trụ H 1 bằng
![]()
![]()
![]()
![]()
Cho lăng trụ lục giác đều ABCDEF.A'B'C'D'E'F'. O và O' là tâm đường tròn ngoại tiếp hai đáy, mặt phẳng (P) đi qua trung điểm của OO' và cắt các cạnh bên của lăng trụ. Chứng minh rằng (P) của lăng trụ đã cho thành hai đa diện có thể tích bằng nhau
Người ta làm tạ tập cơ tay như hình vẽ với hai đầu là hai khối trụ bằng nhau và tay cầm cũng là khối trụ. Biết hai đầu là hai khối trụ đường kính đáy bằng 12, chiều cao bằng 6, chiều dài tạ bằng 30 và bán kính tay cầm là 2. Hãy tính thể tích vật liệu làm nên tạ tay đó.
Đọc tiếp
Người ta làm tạ tập cơ tay như hình vẽ với hai đầu là hai khối trụ bằng nhau và tay cầm cũng là khối trụ. Biết hai đầu là hai khối trụ đường kính đáy bằng 12, chiều cao bằng 6, chiều dài tạ bằng 30 và bán kính tay cầm là 2. Hãy tính thể tích vật liệu làm nên tạ tay đó.

![]()
![]()
![]()
![]()
Cho hai hình vuông ABCD và ABEF có cạnh bằng 1, lần lượt nằm trên hai mặt phẳng vuông góc với nhau. Gọi S là điểm đối xứng với B qua đường thẳng DE. Thể tích của khối đa diện ABCDSEF bằng A.
7
6
B.
11
12
C.
2
3
D.
5
6
Đọc tiếp
Cho hai hình vuông ABCD và ABEF có cạnh bằng 1, lần lượt nằm trên hai mặt phẳng vuông góc với nhau. Gọi S là điểm đối xứng với B qua đường thẳng DE. Thể tích của khối đa diện ABCDSEF bằng
A. 7 6
B. 11 12
C. 2 3
D. 5 6




