Các câu hỏi tương tự
Cho
a
→
và
b
→
là hai vectơ cùng hướng và đều khác vectơ
0
→
. Trong các kết quả sau đây, hãy chọn kết quả đúng: A. B. C. D.
Đọc tiếp
Cho a → và b → là hai vectơ cùng hướng và đều khác vectơ 0 → . Trong các kết quả sau đây, hãy chọn kết quả đúng:
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho A = {0; 1; 2; 3; 4} và B = {2; 3; 4; 5; 6}. Kết quả của phép toán (A\B) ∪ (B\A) là:
A. {0; 1; 5; 6}; B. {1; 2}; C. {2; 3; 4}; D. {5; 6}.
Trong một trận đấu có bốn đội tham gia là A,B,C,D. Trước khi thi đấu, ba bạn Dung, Quang, Trung dự đoán như sau: Dung: B nhì, còn C ba. Quang: A nhì, còn C tư. Trung: B nhất và D nhì.Kết quả, mỗi bạn dự đoán đúng một đội và sai một đội. Hỏi mỗi đội đã đạt giải mấy? A. B nhì, A nhất, C ba, D thứ 4 B. B nhất, A nhì, C thứ 4, D ba C. B nhất, A nhì, C ba, D thứ 4 D. B thứ 4, A ba, Cnhì, D nhất
Đọc tiếp
Trong một trận đấu có bốn đội tham gia là A,B,C,D. Trước khi thi đấu, ba bạn Dung, Quang, Trung dự đoán như sau:
Dung: B nhì, còn C ba.
Quang: A nhì, còn C tư.
Trung: B nhất và D nhì.
Kết quả, mỗi bạn dự đoán đúng một đội và sai một đội. Hỏi mỗi đội đã đạt giải mấy?
A. B nhì, A nhất, C ba, D thứ 4
B. B nhất, A nhì, C thứ 4, D ba
C. B nhất, A nhì, C ba, D thứ 4
D. B thứ 4, A ba, Cnhì, D nhất
Có 100 học sinh tham dự kì thi học sinh giỏi Hóa ( thang điểm 20). Kết quả như sau:
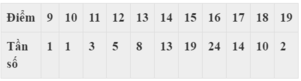
a) Số trung vị là:
A. 15 B. 15,50
C. 16 D. 16,50
b) Mốt là:
A. 14 B. 15
C. 16 D. 17
Câu 4 : Cho tam giác ABC vuông cân tại A và AB =√2 . Tính vectơ CA . vectơ BC . Câu 5 : Cho ABC có trọng tâm G . Biểu diễn vectơ AG theo hai vectơ AB , AC được kết quả là? Câu 6 : Cho các vectơ a,b thỏa mãn|vectơ a | =1 , |vectơ B | =2 , | vectơ a - vectơ b| =3 . Tích vectơ a. vectơ b bằng? Câu 7 : Cho hình vuông ABCD có cạnh bằng a . Tính| vectơ AB - vectơ AD + vectơ CD | .
Cho các tập hợp A {a; b; c; d}; B {b; d; e}; C {a; b; e}. Trong các đẳng thức sau a. A ∩ (B C) (A ∩ B) (A ∩ C). b. A (B ∩ C) (A B) ∩ (A C). c. A ∩ (B C) (A B) ∩ (A C). d. A (B ∩ C) (A B) ∪ (A C). Số đẳng thức sai là A. 1 B. 3 C. 2 D. 4
Đọc tiếp
Cho các tập hợp A = {a; b; c; d}; B = {b; d; e}; C = {a; b; e}. Trong các đẳng thức sau
a. A ∩ (B \ C) = (A ∩ B) \ (A ∩ C).
b. A \ (B ∩ C) = (A \ B) ∩ (A \ C).
c. A ∩ (B \ C) = (A \ B) ∩ (A \ C).
d. A \ (B ∩ C) = (A \ B) ∪ (A \ C).
Số đẳng thức sai là
A. 1
B. 3
C. 2
D. 4
Cho A là tập hợp các ước nguyên dương của 24, B là tập hợp các ước nguyên dương của 18. Xác định tính sai của các kết quả sau:
A. Tập A có 8 phần tử
B. Tập B có 6 phần tử
C. Tập A ∪ B có 14 phần tử
D. Tập B\A có 2 phần tử
Bài 1:Cho các tập hợp: A{a;b;c;d}, B{a;b}. Hãy tìm tất cả các tập X sao cho: B⊂X⊂A.Bài 2:Cho các tập hợp: A{1;2;3;4;5}, B{2;4;6}, C{1;3;5}. Thực hiện các phép toán sau:a)AcupB; AcapB; BcapCb)(AcupB)capC; (AcapB)cupC
Đọc tiếp
Bài 1:Cho các tập hợp: A={a;b;c;d}, B={a;b}. Hãy tìm tất cả các tập X sao cho: B⊂X⊂A.
Bài 2:Cho các tập hợp: A={1;2;3;4;5}, B={2;4;6}, C={1;3;5}. Thực hiện các phép toán sau:
a)A\(\cup\)B; A\(\cap\)B; B\(\cap\)C
b)(A\(\cup\)B)\(\cap\)C; (A\(\cap\)B)\(\cup\)C
Giả sử A và B là hai tập hợp, A ⊂ B và x ∈ B. Mệnh đề nào là sai trong các mệnh đề sau?
A. x ∈ A ⇒ x ∈ A ∩ B
B. x ∈ B \ A ⇒ x ∈ A
C. x ∈ A \ B ⇒ x ∈ A
D. x ∈ A \ B ⇒ x ∈ A








