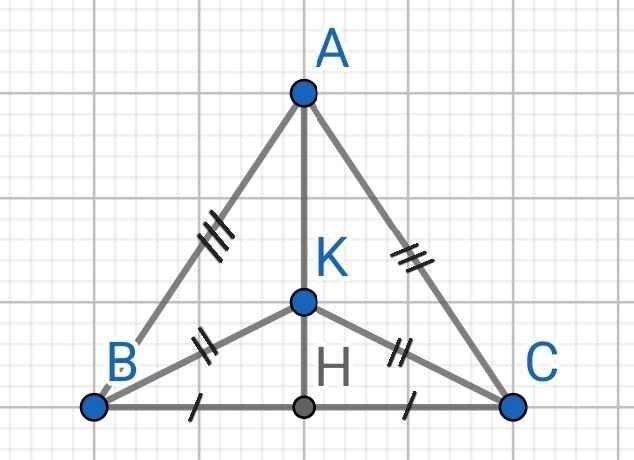
∆ABC cân tại A
⇒ H là trung điểm BC
⇒ AH là đường trung trực của ABC
⇒ AH là đường trung trực của BC
Ta có:
KB = KC (gt)
⇒ K nằm trên đường trung trực của BC
Mà AH là đường trung trực của BC
⇒ K ∈ AH
⇒ A, K, H thẳng hàng
Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm K sao cho BK=BA. Gọi M là trung điểm của đoạn thẳng AK. a) Chứng minh: ∆AMB=∆KMB b) Đường thẳng BM cắt đường thẳng AC tại D. Chứng minh: DK vuông góc với BC. c) Trên tia đối của tia AB lấy điểm H sao cho ah=kc chứng minhh d k thẳng hàng
Cho tam giác ABC có góc A=90 độ; AB<AC; phân giác BE, E thuộc AC. Lấy điểm H thuộc cạnh BC sao cho BH=BA
a) Chứng minh EH vuông góc với BC
b) Chứng minh BE là đường trung trực của AH
c) Đường thẳng EH cắt đường thẳng AB ở K. Chứng minh EK=EC
d) Chứng minh AH//KC
e) Gọi M là trung điểm của KC. Chứng minh ba điểm B, E, M thẳng hàng
tam giác ABC có 3 góc nhọn (AB<AC). M trung điểm AC. Lấy D là trung điểm DB. Chứng minh:
a/ AD=BC
b/ Tam giác ABC = Tam giác CDA
c/ Trên BC lấy H bất kì và AD lấy K bất kì sao cho BH = DK. Chứng minh AH=CK
d/ Chứng minh H,M,K thẳng hàng
1. Cho ∆ABC vuông tại A (AB < AC). Vẽ tia BD là phân giác của góc ABC (D ∈ AC). Trên cạnh BC lấy điểm E sao cho BA = BE.
a. Chứng minh: ∆BAD = ∆BED
b. Từ A kẻ AH ⊥ BC tại H. Chứng minh: AH // DE
c. Trên tia đối của tia ED lấy điểm K sao cho ED = EK. Chứng minh: Góc EKC = góc ABC
2.
Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BE = BA. Phân giác góc B cắt AC tại D.
a. Chứng minh ∆ABD = Đồng ý∆EBD và DE ⊥ BC
b. Gọi K là giao điểm của tia ED và tia BA. Chứng minh AK = EC.
c. Gọi M là trung điểm của KC. Chứng minh ba điểm B, D, M thẳng hàng.
3.
Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm M sao cho BA = BM. Gọi E là trung điểm AM.
a.Chứng minh: ∆ABE = ∆MBE.
b. Gọi K là giao điểm BE và AC. Chứng minh: KM ⊥ BC,
c. Qua M vẽ đường thẳng song song với AC cắt BK tại F. Trên đoạn thẳng KC lấy điểm Q sao cho KQ = MF. Chứng minh: góc ABK = QMC
4
Cho tam giác ABC có AB = AC, lấy M là trung điểm của BC.
a) Chứng minh ∆ABM = ∆ACM
b) Kẻ ME ⊥ AB tại Em kẻ MF ⊥ AC tại F. Chứng minh AE = AF.
c) Gọi K là trung điểm của EF. Chứng minh ba điểm A, K, M thẳng hàng
d) Từ C kẻ đương thẳng song song với AM cắt tia BA tại D. Chứng minh A là trung điểm của BD.
Cho tam giác ABC có góc A=90 độ, AB=AC,phân giác BE,E thuộc AC. Lấy H thuộc cạnh BC sao cho BH=BA
a)Chứng minh EH vuông góc BC
b)Chứng minh BE là đường trung trực của AH
c)Đường thẳng EH cắt đường thẳng AB ở K. Chứng minh EK=EC
d)Chứng minh AH//KC
e)Gọi M là trung điểm của KC.Chứng minh ba điểm B,E,M thẳng hàng
Cho tam giác ABC vuông tại A có AB < AC. Lấy D là trung điểm của AC,
trên tia đối của tia DB lấy điểm E sao cho DE = DB.
a) Chứng minh: tam giác ADB = tam giác CDE.
b) Vẽ đường thẳng vuông góc với AC tại D cắt BC tại K.
Chứng minh AK = KC và góc ABK= KAB
c) Trên tia KD lấy điểm H sao cho D là trung điểm của KH.
Chứng minh A, H, E thẳng hàng.
giúp mik vs, tks
Cho tam giác ABC có K là trung điểm của AB,E là trung điểm của AC. Trên tia đối của tia KC lấy điểm M sao cho KM = KC. Trên tia đối của tia EB lấy điểm N sao cho EN = EB. Chứng minh rằng :
a) AM = AN.
b) Ba điểm M, A, N thẳng hàng.
Cho tam giác ABC, M là trung điểm của AC. Trên tia đối của tia MB lấy D sao cho MB=MD. Chứng minh rằng:
a, Tam giác AMB=tam giác CMD
b, AD//BC
c, Gọi H là trung điểm của AB, K là trung điểm của CD. Chứng minh 3 điểm H, M, K thẳng hàng
Cho tam giác ABC vuông tại A, có AB = 3cm, AC = 4cm. M là trung điểm AC. Trên tia đối của tia MB, lấy điểm D sao cho MB = MD. N là trung điểm CD, BN cắt AC tại H. K là trung điểm BC.
a) Tính CH.
b) Chứng minh ba điểm K, H, D thẳng hàng.
