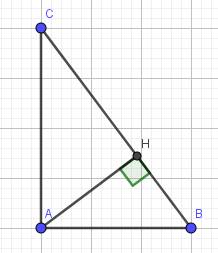
\(\Delta ABC\) vuông tại A, đường cao AH
\(\Rightarrow AH.BC=AB.AC\)
\(\Rightarrow AB=\dfrac{AH.BC}{AC}=\dfrac{12.25}{AC}=\dfrac{300}{AC}\)
Lại có:
\(AB^2+AC^2=BC^2=25^2=625\left(Pytago\right)\)
\(\Rightarrow\left(\dfrac{300}{AC}\right)^2+AC^2=625\)
\(\Leftrightarrow\dfrac{90000}{AC^2}+AC^2=625\)
\(\Leftrightarrow AC^4+90000=625AC^2\)
\(\Leftrightarrow AC^4-625AC^2+90000=0\)
\(\Leftrightarrow AC^4-225AC^2-400AC^2+90000=0\)
\(\Leftrightarrow\left(AC^4-225AC^2\right)-\left(400AC^2-90000\right)=0\)
\(\Leftrightarrow AC^2\left(AC^2-225\right)-400\left(AC^2-225\right)=0\)
\(\Leftrightarrow\left(AC^2-225\right)\left(AC^2-400\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}AC^2-225=0\\AC^2-400=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}AC^2=225\\AC^2=400\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}AC=15\\AC=20\end{matrix}\right.\)
*) \(AC=15cm\)
\(\Rightarrow AB=\dfrac{300}{15}=20\left(cm\right)\)
*) \(AC=20cm\)
\(\Rightarrow AB=\dfrac{300}{20}=15\left(cm\right)\)
Vậy AB = 20 cm; AC = 15 cm
Hoặc AB = 15 cm; AC = 20 cm












