Các câu hỏi tương tự
Cho hàm số `y=x^3-3x+1` có đồ thị `(C)`.Tìm tất cả giá trị của a để qua điểm `A(a;-1)` kẻ 3 tiếp tuyến đến đồ thị `(C)` sao cho trong đó có 2 tiếp tuyến vuông góc với nhau.Ai giúp mình với ạ!!
Cho hàm số y = a x + b x - 1 có đồ thị cắt trục tung tại A(0; -1), tiếp tuyến tại A có hệ số góc k = -3. Các giá trị của a, b là
A. a = 1; b = 1
B. a = 2; b = 1
C. a = 1; b = 2
D. a = 2; b = 2
Cho hàm số
y
a
x
+
b
x
-
1
có đồ thị cắt trục tung tại A(0; -1), tiếp tuyến tại A có hệ số góc k -3. Các giá trị của a, b là A. a 1; b 1 B. a 2; b 1 C. a 1; b 2 D. a 2; b 2
Đọc tiếp
Cho hàm số y = a x + b x - 1 có đồ thị cắt trục tung tại A(0; -1), tiếp tuyến tại A có hệ số góc k = -3. Các giá trị của a, b là
A. a = 1; b = 1
B. a = 2; b = 1
C. a = 1; b = 2
D. a = 2; b = 2
Cho hàm số y=\(x^3-3x^2-1\)có đồ thị (C).Điểm M(a;b) trên(C) có hoành độ thuộc [2;3] sao cho tiếp tuyến của (C) tại M có hệ số góc lớn nhất.Khi đó, S=a+b=?
cho hàm số \(\dfrac{-x+2}{x-1}\) có đồ thị (C) và điểm A(a;1) . Gọi S là tập hợp tất cả các giá trị thực củ tham số a để có đúng 1 tiếp tuyến của (C) đi qua A. Tổng tất cả các giá trị của S là
Cho hàm số y = ax3 + bx2 + cx + d (a khác 0) , có đồ thị (C). Tìm tập hợp tất cả các giá trị thực của tham số a để tiếp tuyến của (C) tại điểm x0 = -b/3a có hệ số góc nhỏ nhất.
Giúp mình cách làm với ạ 😍
a) tìm hệ số góc của tiếp tuyến của đồ thị hàm số y=-x^3+3x-2 (c) tại điểm có hoành độ -3
b) viết phương trình tiếp tuyến của đồ thị hàm số (c) trên tại điểm ( ứng với tiếp điểm ) có hoành độ -3
Cho hàm số y = x3 + 3mx2 + (m + 1)x + 1 (1), m là tham số thực. Tìm các giá trị của m để tiếp tuyến của đồ thị của hàm số (1) tại điểm có hoành độ x = -1 đi qua điểm A(1; 2).
A: 1
B: -1
C: 3/4
D: 5/8
Cho hàm số
y
x
3
-
3
x
+
2
có đồ thị (C) . Gọi d là đường thẳng đi qua A(3;20) và có hệ số góc m. Giá trị của m để đường thẳng cắt (C) tại 3 điểm phân biệt là
Đọc tiếp
Cho hàm số y = x 3 - 3 x + 2 có đồ thị (C) . Gọi d là đường thẳng đi qua A(3;20) và có hệ số góc m. Giá trị của m để đường thẳng cắt (C) tại 3 điểm phân biệt là
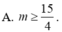
![]()
![]()
![]()







