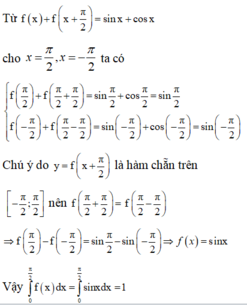Các câu hỏi tương tự
Tìm hàm số F(x) sao cho F’(x) f(x) nếu:f(x) 1/(cosx)2 với x ∈ ((-π)/2; π/2).
f
x
1
cos
x
2
v
ớ
i
x
∈
-
π
2
;
π...
Đọc tiếp
Tìm hàm số F(x) sao cho F’(x) = f(x) nếu:
f(x) = 1/(cosx)2 với x ∈ ((-π)/2; π/2). f x = 1 cos x 2 v ớ i x ∈ - π 2 ; π 2
Cho hàm f(x) có đạo hàm trên đoạn
[
0
;
π
]
,
f
(
0
)
π
,
∫
0
π
f
(
x
)
dx
3
π
. Tính
f
(
π
)
Đọc tiếp
Cho hàm f(x) có đạo hàm trên đoạn [ 0 ; π ] , f ( 0 ) = π , ∫ 0 π f ' ( x ) dx = 3 π . Tính f ( π )
![]()
![]()
![]()
![]()
Cho hàm số yf(x) liên tục trên
ℝ
và có đồ thị như hình bên. Phương trình f( 2 sin x) m có đúng ba nghiệm phân biệt thuộc đoạn
-
π
;
π
khi và chỉ khi A.
m
∈
-
3
;
1
B.
m
∈
-...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình bên. Phương trình f( 2 sin x) = m có đúng ba nghiệm phân biệt thuộc đoạn - π ; π khi và chỉ khi
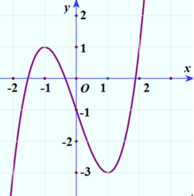
A. m ∈ - 3 ; 1
B. m ∈ - 3 ; 1
C. m ∈ [ - 3 ; 1 )
D. m ∈ ( - 3 ; 1 ]
Cho f(x)
log
5
(
sin
x
)
,
x
∈
(
0
;
π
/
2
)
. Tính f(x)
Đọc tiếp
Cho f(x)= log 5 ( sin x ) , x ∈ ( 0 ; π / 2 ) . Tính f'(x)
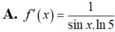
![]()
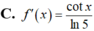
![]()
Giá trị lớn nhất của hàm số f(x) = sin x + cos 2x trên [0; π ] là
A. 5 4
B. 1
C. 2
D. 9 8
Cho hàm số f(x) có đạo hàm liên tục trên đoạn
0
;
π
thỏa mãn:
∫
0
π
f
x
d
x
∫
0
π
cos
x
.
f
x
d
x
π
/...
Đọc tiếp
Cho hàm số f(x) có đạo hàm liên tục trên đoạn 0 ; π thỏa mãn: ∫ 0 π f ' x d x = ∫ 0 π cos x . f x d x = π / 2 và f π / 2 = 1 . Khi đó tích phân ∫ 0 π / 2 f x d x bằng
A.0.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm f(x) có đạo hàm trên đoạn
0
;
π
;
∫
0
π
f
(
x
)
d
x
3
π
Tính
f
(
π
)
Đọc tiếp
Cho hàm f(x) có đạo hàm trên đoạn 0 ; π ; ∫ 0 π f ' ( x ) d x = 3 π Tính f ( π )
![]()
![]()
![]()
![]()
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:a) f(x)
(
25
-
x
2
)
trên đoạn [-4; 4]b) f(x) |
x
2
– 3x + 2| trên đoạn [-10; 10]c) f(x) 1/sinx trên đoạn [π/3; 5π/6]d) f(x) 2sinx + sin2x trên đoạn [0; 3π/2]
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) f(x) = ( 25 - x 2 ) trên đoạn [-4; 4]
b) f(x) = | x 2 – 3x + 2| trên đoạn [-10; 10]
c) f(x) = 1/sinx trên đoạn [π/3; 5π/6]
d) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
Cho hình phẳng H giới hạn bởi các đường: y f(x), y 0, x b và x a (trong đó hàm số f(x) liên tục trên đoạn [b,a]). Thể tích khối tròn xoay tạo nên bởi phép quay H quanh trục Ox được cho bởi công thức:A.
π
∫
a
b
f
2
x
d
x
B.
∫...
Đọc tiếp
Cho hình phẳng H giới hạn bởi các đường: y = f(x), y = 0, x = b và x = a (trong đó hàm số f(x) liên tục trên đoạn [b,a]). Thể tích khối tròn xoay tạo nên bởi phép quay H quanh trục Ox được cho bởi công thức:
A. π ∫ a b f 2 x d x B. ∫ a b f 2 x d x
C. π ∫ b a f 2 x d x D. ∫ b a π f x 2 d x
Cho hàm số f(x) có đạo hàm liên tục trên
0
;
π
. Biết
f
0
2
e
và f(x) luôn thỏa mãn đẳng thức
f
x
+
sinx
.
f
x
cosx
.
e
cosx
,
∀
x
∈
0
;...
Đọc tiếp
Cho hàm số f(x) có đạo hàm liên tục trên 0 ; π . Biết f 0 = 2 e và f(x) luôn thỏa mãn đẳng thức f ' x + sinx . f x = cosx . e cosx , ∀ x ∈ 0 ; π . Tính I = ∫ 0 π f x dx (làm tròn đến phần trăm).
A. I ≈ 6,55
B. I ≈ 17,30
C. I ≈ 10,31
D. I ≈ 16,91