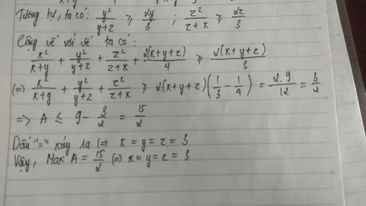Ta có:\(A=\dfrac{xy}{x+y}+\dfrac{yz}{y+z}+\dfrac{zx}{z+x}\)
\(=\dfrac{x\left(x+y\right)-x^2}{x+y}+\dfrac{y\left(y+z\right)-y^2}{y+z}+\dfrac{z\left(z+x\right)-z^2}{z+x}\)
\(=\left(x+y+z\right)-\left(\dfrac{x^2}{x+y}+\dfrac{y^2}{y+z}+\dfrac{z^2}{z+x}\right)\)
Ta có:\(\dfrac{x^2}{x+y}+\dfrac{x+y}{9}\ge2\sqrt{\dfrac{x^2}{x+y}.\dfrac{x+y}{9}}=\dfrac{2x}{3}\)
Tương tự,ta có:\(\dfrac{y^2}{y+z}+\dfrac{y+z}{9}\ge\dfrac{2y}{3};\dfrac{z^2}{z+x}+\dfrac{z+x}{9}\ge\dfrac{2z}{3}\)
Cộng vế với vế ta có:
\(\dfrac{x^2}{x+y}+\dfrac{y^2}{y+z}+\dfrac{z^2}{z+x}+\dfrac{2\left(x+y+z\right)}{4}\ge\dfrac{2\left(x+y+z\right)}{3}\)
\(\Leftrightarrow\dfrac{x^2}{x+y}+\dfrac{y^2}{y+z}+\dfrac{z^2}{z+x}\ge\dfrac{2\left(x+y+z\right)}{3}-\dfrac{2\left(x+y+z\right)}{4}=\dfrac{2.9}{3}-\dfrac{9}{2}=\dfrac{3}{2}\)
\(\Rightarrow A\le9-\dfrac{3}{2}=\dfrac{15}{2}\)
Dấu "=" xảy ra ⇔ x=y=z=3
Vậy,Max A=\(\dfrac{15}{2}\) ⇔ x=y=z=3