Xét tam giác vuông EFD có:
FM là đường trung tuyến ứng với cạnh huyền CD
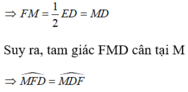
Ta có:
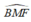 là góc ngoài tại đỉnh M của tam giác FMD nên:
là góc ngoài tại đỉnh M của tam giác FMD nên:

Xét tứ giác BCMF có:
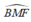 và
và 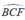 và cùng nhìn cạnh BF dưới một góc bằng nhau
và cùng nhìn cạnh BF dưới một góc bằng nhau
Suy ra, tứ giác BCMF nội tiếp được.

Xét tam giác vuông EFD có:
FM là đường trung tuyến ứng với cạnh huyền CD
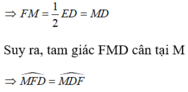
Ta có:
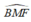 là góc ngoài tại đỉnh M của tam giác FMD nên:
là góc ngoài tại đỉnh M của tam giác FMD nên:

Xét tứ giác BCMF có:
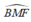 và
và  và cùng nhìn cạnh BF dưới một góc bằng nhau
và cùng nhìn cạnh BF dưới một góc bằng nhau
Suy ra, tứ giác BCMF nội tiếp được.
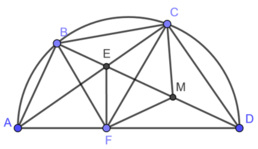
Cho tứ giác ABCD nội tiếp nửa đường tròn đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Kẻ EF vuông góc với AD. Gọi M là trung điểm của DE. Chứng minh rằng: Các tứ giác ABEF, DCEF nội tiếp được
Cho tứ giác ABCD nội tiếp nửa đường tròn đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Kẻ EF vuông góc AD tại F. Gọi M là trung điểm DE. Chứng minh:
a) Các tứ giác ABEF, DCEF nội tiếp
b) CA là phân giác góc BCF
c) Tứ giác BCMF nội tiếp
Cho tứ giác ABCD nội tiếp nửa đường tròn đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Kẻ EF vuông góc với AD. Gọi M là trung điểm của DE. Chứng minh rằng: Tia CA là tia phân giác của góc BCF
Cho tứ giác ABCD nội tiếp nửa đưởng tròn đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Vẽ EF vuông góc vớI AD. Chứng minh:
a, Tứ giác ABEF, DCEF nội tiếp
b, CA là phân giác của góc BCF
c, Gọi M là trung điểm của DE, chứng minh tứ giác BCMF nội tiếp.
MỌI NGƯỜI AI BIẾT LÀM GIẢI GIÚP MÌNH PHẦN C. CẢM ƠN NHIỀU <3
Cho tứ giác ABCD nội tiếp đường tròn đường kính AD. Hai đường chéo
ac và BD cắt nhau tại E. Kẻ EF vuông góc AD. Gọi M là trung điểm của AE. Chứng minh rằng:
a) Thứ giác ABEF nội tiếp
b) BD là phân giác góc CBF
Cho tứ giác ABCD nội tiếp nửa đường tròn đường kính AD , hai đường chéo AC và BD cắt nhau tại E . Vẽ EF vuông góc với AD , gọi M là trung điểm của DE. Chứng Minh rằng :
a)Các tứ giác ABEF và DCEF nội tiếp được
b) Tia CA là phân giác của góc BCF
Cho tứ giác ABCD nội tiếp nửa đường tròn (O) đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Kẻ EF vuông góc với AD (F\(\in\) AD; F \(\ne\)O).
a) Chứng minh: Tứ giác ABEF nội tiếp được;
b) Chứng minh: Tia CA là tia phân giác của góc BCF;
c) Gọi M là trung điểm của DE. Chứng minh: CM.DB = DF.DO.
Cho tứ giác ABCD nội tiếp đường tròn tâm O đường kính AD hai đường chéo AC và BD cắt nhau tại E kẻ EF vuông góc ad a) Chứng minh tứ giác ECDF nội tiếp Xác định tâm I b) Chứng minh CA là phân giác của góc BCF c) Chứng minh tứ giác bcef nội tiếp
Cho tứ giác ABCD nội tiếp nửa đường tròn đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Vẽ EF vuông góc với AD ( F thuộc AD), CF cắt đường trong tại M. Chứng minh rằng:
a) các tứ giác ABEF;DCEF nội tiếp đường tròn.
B) tia CA là tia phân giác của góc BCF
C) BM vuông góc AD