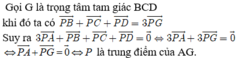Các câu hỏi tương tự
Cho ba điểm A (0,6) B(-3,2) C(5,-1)
A ) chứng minh rằng A , B ,C lập thành một tam giác
B ) Tìm tọa độ điểm M ,N , P lần lượt là trung điểm của AB , BC và CA
C ) Tìm tọa độ điểm D sao cho A là trọng tâm tam giác BCD
D ) Tìm tọa độ điểm E sao cho tứ giác ABEC là hình bình hành
Cho tứ giác ABCD. Gọi I là trung điểm BC. Xác định điểm M sao cho
2
M
A
→
+
M
B
→
+
M
C
→
0
→
A. M là trung điểm BI B. M là trung điểm AC C. M là trung điểm AB D. M là...
Đọc tiếp
Cho tứ giác ABCD. Gọi I là trung điểm BC. Xác định điểm M sao cho 2 M A → + M B → + M C → = 0 →
A. M là trung điểm BI
B. M là trung điểm AC
C. M là trung điểm AB
D. M là trung điểm AI
Câu 1: Cho tam giác ABC có A(3,2); B(4,1) và C(1,5).a/ Tìm tọa độ trọng tâm G của tam giác ABC.b/ Tìm tọa độ điểm D để ABCD là hình bình hànhc/ Tìm tọa độ sao cho Câu 2: Cho ngũ giác ABCDE. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DE. I, J là trung điểm của MP, NQ. Chứng minh rằng:
Đọc tiếp
Câu 1: Cho tam giác ABC có A(3,2); B(4,1) và C(1,5).
a/ Tìm tọa độ trọng tâm G của tam giác ABC.
b/ Tìm tọa độ điểm D để ABCD là hình bình hành
c/ Tìm tọa độ ![]() sao cho
sao cho ![]()
Câu 2: Cho ngũ giác ABCDE. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DE. I, J là trung điểm của MP, NQ. Chứng minh rằng: 
Cho tam giác ABC có trọng tâm G. M, N lần lượt là trung điểm của AB, BC. Lấy 2 điểm I, J sao cho 2overrightarrow{IA}+3overrightarrow{IC}overrightarrow{0}, 2overrightarrow{JA}+5overrightarrow{JB}+3overrightarrow{JC}overrightarrow{0}a) CM: M, N, J thẳng hàng với J là trung điểm của BIb) Gọi E là điểm thuộc AB sao cho overrightarrow{AE}k.overrightarrow{AB}. Xác định k sao cho C, E, J thẳng hàng
Đọc tiếp
Cho tam giác ABC có trọng tâm G. M, N lần lượt là trung điểm của AB, BC. Lấy 2 điểm I, J sao cho \(2\overrightarrow{IA}+3\overrightarrow{IC}=\overrightarrow{0}\), \(2\overrightarrow{JA}+5\overrightarrow{JB}+3\overrightarrow{JC}=\overrightarrow{0}\)
a) CM: M, N, J thẳng hàng với J là trung điểm của BI
b) Gọi E là điểm thuộc AB sao cho \(\overrightarrow{AE}=k.\overrightarrow{AB}\). Xác định k sao cho C, E, J thẳng hàng
cho tam giác ABC gọi G là trọng tâm cuả tam giác ; I là điểm xác định bởi →IA+2*→IB=→0; j là điểm trên BC sao cho →JB=x* →JC
a,biểu diễn →CI, →CJ theo →CA, →CB
b,biểu diễn→IJ theo →CA và →CB
c,tìm x để IJ//CG
Câu 8: Cho hình bình hành ABCD. Gọi M, N lần lượt là trung điểm của AD và BC, có bao nhiêu vectơ bằng với DM từ các điểm đã cho? A. 3. B. 4. C. 5. D. Câu 9: Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chọn khẳng định đúng trong các khẳng định sau.A. AD BC . B. MQ PN . C. MN QP . D. AB DC .Câu 10: Cho tam giác ABC với trực tâm H, D là điểm đối xứng với B qua tâm O của đường tròn ngoại tiếp tam giác ABC. Khẳng định nào sau đây là đúngA. HA CD và AD CH .B....
Đọc tiếp
Câu 8: Cho hình bình hành ABCD. Gọi M, N lần lượt là trung điểm của AD và BC, có bao nhiêu vectơ bằng với DM từ các điểm đã cho? A. 3. B. 4. C. 5. D. Câu 9: Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chọn khẳng định đúng trong các khẳng định sau.
A. AD BC . B. MQ PN . C. MN QP . D. AB DC .
Câu 10: Cho tam giác ABC với trực tâm H, D là điểm đối xứng với B qua tâm O của đường tròn ngoại tiếp tam giác ABC. Khẳng định nào sau đây là đúng
A. HA CD và AD CH .
B. HA CD và DA HC .
C. HA CD và AD HC .
D. HA CD và AD HC và OB OD .
Câu 1: Cho ABCD là hình vuông cạnh bằng 1. Khi đó độ dài của AC bằng
A. 1. B. 2. C. 2. D. 3.
Câu 2: Cho tam giác ABC vuông tại C có cạnh AC cm BC cm 4 , 3 . Độ dài của vectơ AB là
A. 7 . cm B. 6 . cm C. 5 . cm D. 4 . cm
Câu 3: Cho hình vuông ABCD tâm O, cạnh 2a. Độ dài vectơ DO bằng
A. 2 2. a B. 2 . 2 a C. a 2. D. 2 2. a
Câu 4: Cho đoạn thẳng AB cm 10 , điểm C thỏa mãn AC CB . Độ dài vectơ AC là
A. 10 . cm B. 5 . cm C. 20 . cm D. 15 . c
trong mặt phẳng tọa độ oxy, cho 3 điểm A (3;3) B (4;-2) C(-1;-1)
1. tính vecto AB và vecto BC từ đó suy ra A,B, C là ba đỉnh của một tam giác
2. Tìm tọa độ điểm M thỏa mãn vecto MA + 4MB - MC = 0
3. Cho hình bình hành ABCD. Gọi I là trung điểm cạnh bC và E là điểm xác định bởi vecto AE = 2/3AC. CMR: vecto DI = AB - 1/2AD và 3 điểm D, E, I thẳng hàng
Cho tam giác ABC, A(4;0) B(2;-4) C(0;-2). Gọi G là trọng tâm tam giác ABC. GỌi M, N, P lần lượt là trung điểm các cạnh BC, CA, AB. Chứng minh tam giác ABC, tam giác MNP có cùng trọng tâm
Cho điểm A(1;-3), B(3;1), C(-2;0)
a, Tìm tọa độ trung điểm của AB, BC, CA.
b, Tìm tọa độ trọng tâm tam giác ABC
c, Tính d, Tìm D để ABCD là hình bình hành