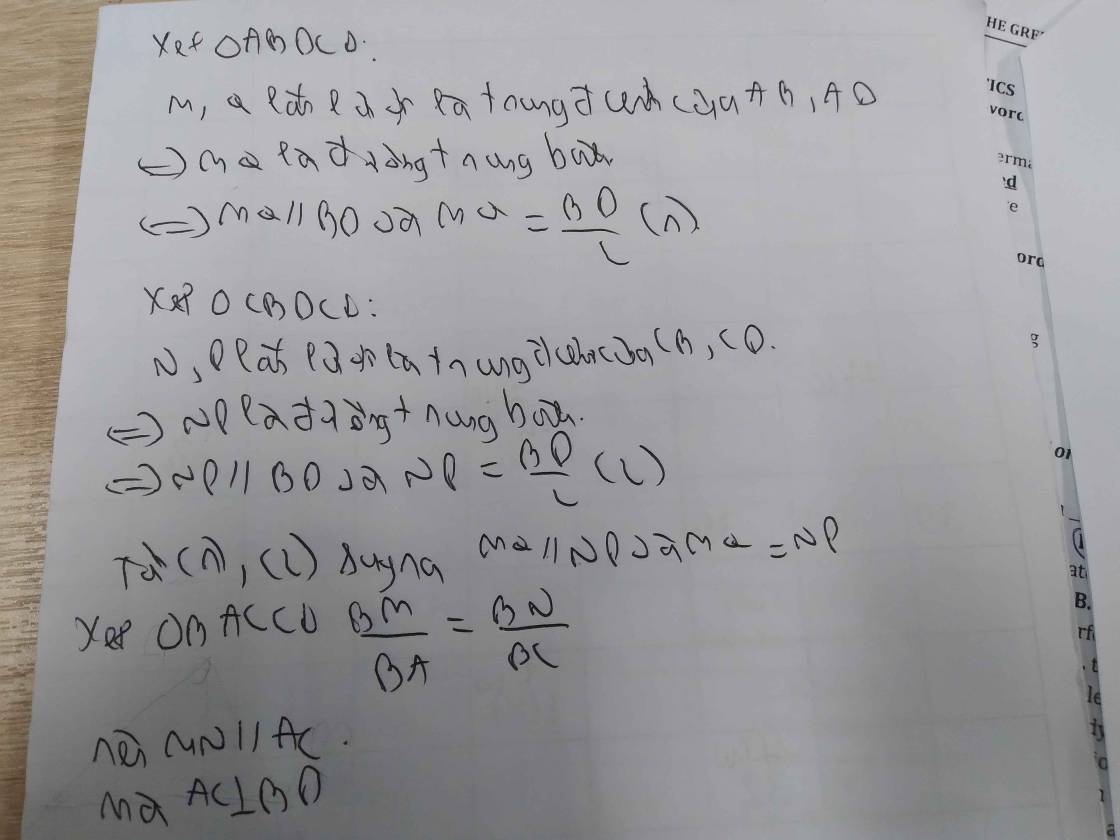Các câu hỏi tương tự
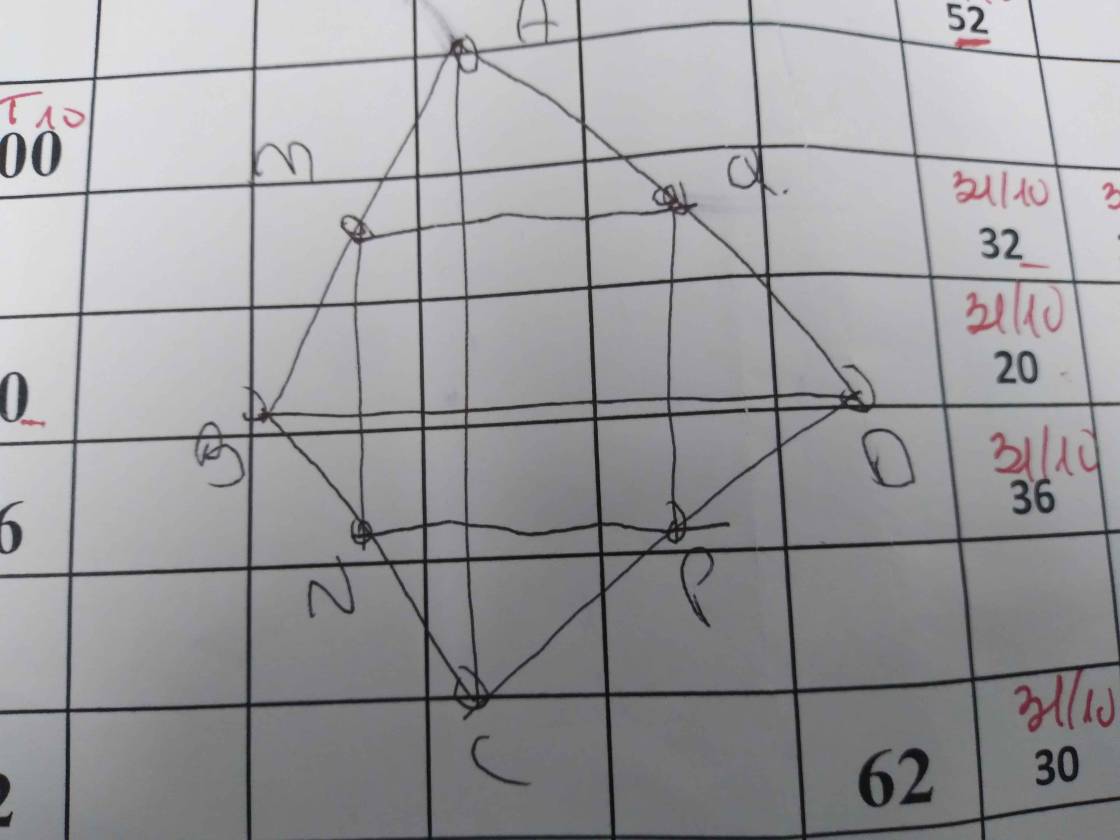
cho tứ giác ABCD có hai đường chéo AC vuông BD.Gọi M,N,P,Q lần lượt là trung điểm của AB,BC,CD,DA.Chứng minh rằng:4 điểm M,N,P,Q cùng thuộc 1 đường tròn
cho tứ giác ABCD có hai đường chéo AC vuông góc BD.Gọi M,N,P,Q lần lượt là trung điểm của AB,BC,CD,DA.Chứng minh rằng:4 điểm M,N,P,Q cùng thuộc 1 đường tròn
Cho tứ giác abcd có 2 đường chéo ac bd
4 điểm m n p q lần lượt là trung điểm mỗi cạnh ab bc cd ad
Chứng minh 4 điểm cùng nằm trên 1 đường tròn
Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh M, N, P, Q cùng nằm trên một đường tròn
Bài 1 : Cho hình vuông ABCD có cạnh bằng 3 cm . Chứng minh rằng : 4 đỉnh của hình vuông ABCD cùng nằm trên 1 đường tròn . Hãy tính bán kính đường tròn đó Bài 2 : Cho tam giác nhọn ABC . Vẽ đường tròn tâm O , bán kính BC , nó cắt các cạnh AB, AC theo thứ tự ở D và E a)CMR: CD vuông góc với AB , BE vuông góc với AC b) gọi K là giao điểm của BE và CD. Chứng minh AK vuông góc BCBài 3:Cho hình thang ABCD , AB//CD, ABCD , có góc Cgóc D60 độ , CD2AD . Chứng minh 4 điểm A, B, C, D cùng thuộc 1 đường trò...
Đọc tiếp
Bài 1 : Cho hình vuông ABCD có cạnh bằng 3 cm . Chứng minh rằng : 4 đỉnh của hình vuông ABCD cùng nằm trên 1 đường tròn . Hãy tính bán kính đường tròn đó
Bài 2 : Cho tam giác nhọn ABC . Vẽ đường tròn tâm O , bán kính BC , nó cắt các cạnh AB, AC theo thứ tự ở D và E
a)CMR: CD vuông góc với AB , BE vuông góc với AC
b) gọi K là giao điểm của BE và CD. Chứng minh AK vuông góc BC
Bài 3:Cho hình thang ABCD , AB//CD, AB<CD , có góc C=góc D=60 độ , CD=2AD . Chứng minh 4 điểm A, B, C, D cùng thuộc 1 đường tròn. Tính diện tích đường tròn đó biết CD=4cm
Bài 4:Cho tam giác ABC vuông tại A. Trên AB, AC lần lượt lấy các điểm D, E . Gọi M, N, P, Q lần lượt là trung điểm của DE , EB, BC, CD. Chứng minh 4 điểm M, N, P, Q cùng thuộc 1 đường tròn
1.Cho tứ giác ABCD ngoại tiếp đường tròn tâm O. Gọi M,N,P,Q là các tiếp điểm của đường tròn tâm O với AB,BC,CD,DA. CMR NP,MQ,BD đồng quy
2. Cho HBH ABCD. Lấy S trong HBH. Qua S kẻ các đường thẳng song song với AB cắt AD,BC lần lượt tại M,P. kẻ đường thẳng song song với AD cắt AB,CD lần lượt tại N,Q. Chứng minh AS,PQ,DP đồng quy tại một điểm.
cho hình vuông ABCD.các điểm M,N lần lượt thuộc BC,CD sao cho góc MAN=45 độ. gọi P,Q lần lượt là giao điểm của BD với AN và AM.chứng ming rằng:
các tứ giác ABMN,ADNQ,MNPQ nội tiếp
5 điểm C,M,N,P,Q cung thuộc một đường tròn
PA=PM
QA=QN
Cho tứ giác ABCD có hai đương chéo AC và BD vuông góc với nhau. Gọi M, N, R, S lần lượt là trung điểm của AB, BC, CD, DA. Cm 4 điểm M, N, R, S cùng thuộc 1 đương tròn
Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau. gọi M và N lần lượt là trung điểm của AB và AD. Kẻ ME vuông góc với CD tại E, NF vuông góc với BC tại F. chứng minh M,N,E,F cùng thuộc một đường tròn.